Trapèze

Pour les articles homonymes, voir Trapèze (homonymie).

Trapèze
Trapèze avec sa paire de côtés non-parallèles de longueurs b et d, sa paire de côtés parallèles, (c la longueur de la petite base et a celle de la grande base), ses sommets A, B, C et D, sa hauteur de longueur h et le pied H de celle-ci.
Type	Polygone
Angle interne	Variable
Aire	${\displaystyle {\frac {(a+c)h}{2}}}$
Périmètre	${\displaystyle a+b+c+d}$
Propriétés	Constructible
modifier

Un trapèze est un quadrilatère possédant deux côtés opposés parallèles. Ces deux côtés parallèles sont appelés bases.

Avec cette définition, les quadrilatères ABCD et ABDC de la figure sont tous deux des trapèzes (dont les côtés (AB) et (CD) sont parallèles).

Certains auteurs imposent comme condition supplémentaire la convexité du quadrilatère, ce qui revient à exclure les « trapèzes croisés » tels que ABDC.

Propriétés

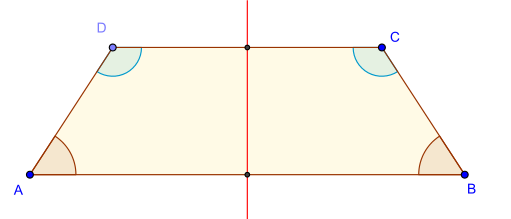
Un quadrilatère convexe est un trapèze si et seulement s’il possède une paire d’angles consécutifs de somme égale à 180°, soit π radians. La somme des deux autres angles est alors la même. Par exemple dans la figure ci-dessus, les deux paires d'angles ont pour sommets (A,D) et (B,C).

Attention : dans un trapèze, la somme de deux angles consécutifs n'est pas toujours égale à 180° (exemple ici : les angles de sommets A et B).

Cas particuliers

• Un trapèze est qualifié de trapèze rectangle s’il possède au moins un angle droit (il en possède alors au moins deux, consécutifs).

• Un trapèze est qualifié d’isocèle^[1] lorsqu'il vérifie l'une des propriétés équivalentes suivantes :
  • deux angles adjacents à une même base sont égaux ;
  • les deux bases du trapèze ont la même médiatrice, et celle-ci est un axe de symétrie du trapèze ;
  • c'est un quadrilatère inscriptible (c'est-à-dire dont les sommets sont cocycliques).

• Un trapèze (non croisé) dont les bases ont la même longueur est un parallélogramme, c'est-à-dire que ses deux autres côtés sont aussi parallèles.
• Les trapèzes dont les deux côtés qui ne sont pas les bases ont la même longueur sont les trapèzes isocèles et les parallélogrammes.
• Les quadrilatères qui sont à la fois des trapèzes isocèles et des parallélogrammes sont les rectangles.
• Un trapèze qui est un quadrilatère circonscriptible (c'est-à-dire qui possède un cercle inscrit) est appelé trapèze circonscriptible.

Aire du trapèze

En fonction des bases et de la hauteur

L’aire du trapèze vaut le produit de sa hauteur h par la demi-somme de ses bases a et c, c'est-à-dire

${\displaystyle S={\dfrac {(a+c)}{2}}h}$.

On obtient ce résultat ^[2],[3] en découpant le trapèze en deux triangles le long d'une diagonale, lesquels ont pour hauteur h, et chacun une des deux bases a et c. Donc ${\displaystyle S={\dfrac {ah}{2}}+{\dfrac {ch}{2}}={\dfrac {(a+c)}{2}}h}$

On peut aussi considérer le rectangle construit à partir des milieux des côtés, qui a même aire que le trapèze (cf. figure ci-contre). Comme ${\displaystyle IJ={\frac {a+c}{2}}}$ (car ${\displaystyle {\overrightarrow {IJ}}={\frac {{\overrightarrow {AB}}+{\overrightarrow {DC}}}{2}}}$), ${\displaystyle S=IJ.h={\dfrac {(a+c)}{2}}h}$.

Autre démonstration en considérant le parallélogramme obtenu après symétrie de centre le milieu d'un des côtés non parallèles.

ABCD est un trapèze de grande base a = AB et de petite base c = CD.

Les points A, B et D’ sont alignés comme les points D, C et A’.

(BD’) est parallèle à (A’C). BD’A’C est un trapèze de même aire que ABCD et l'on a : grandes bases : a = AB = A’C, petites bases : c = CD = BD’, hauteur : h = CH.

(AD) est parallèle à (A’D’). AD’A’D est un parallélogramme de base AD’ = a + c. Aire(AD’A’D) = AD’ × DH = (a + c) × h.

Or Aire(AD’A’D) = Aire(ABCD) + Aire(BD’A’C) = 2 Aire(ABCD), soit 2 Aire(ABCD) = (a + c) × h.

On retrouve Aire(ABCD) = ${\displaystyle {\dfrac {(a+c)h}{2}}}$.

En fonction des longueurs des côtés

L'aire du trapèze est égale à l'aire d'un triangle de côtés de longueurs ${\displaystyle |a-c|,b,d}$, multipliée par ${\displaystyle {\frac {a+c}{a-c}}}$, ce qui, compte tenu de la formule de Héron, donne une formule de l'aire du trapèze lorsque ne sont connues que les quatre longueurs a, b, c, d des quatre côtés ^[4],[5] :

${\displaystyle S={\frac {a+c}{|a-c|}}.{1 \over 4}{\sqrt {(|a-c|+b+d)(|a-c|+b-d)(|a-c|-b+d)(-|a-c|+b+d)}}}$,

où a et c représentent les longueurs (supposées distinctes) des deux bases.

La hauteur peut donc être exprimée en fonction des longueurs des côtés par la relation :

${\displaystyle h^{2}={\frac {(|a-c|+b+d)(|a-c|+b-d)(|a-c|-b+d)(-|a-c|+b+d)}{4(a-c)^{2}}}}$.

Barycentre du trapèze

Le centre de masse d'un trapèze de bases ${\displaystyle a}$ et ${\displaystyle b}$ et de hauteur ${\displaystyle h}$ est situé sur la médiane joignant les deux bases et à une distance ${\displaystyle {\frac {h}{3}}\times {\frac {a+2b}{a+b}}}$ de la base de longueur ${\displaystyle a}$. C'est le barycentre des milieux ${\displaystyle I=I_{a}}$ et ${\displaystyle J=I_{b}}$ pondérés respectivement par ${\displaystyle 2a+b}$ et ${\displaystyle 2b+a}$.

La droite passant par le centre de masse du trapèze et parallèle aux bases découpe un segment dont la longueur correspond à la centroidal mean (moyenne barycentrique) des deux bases^[6] : ${\displaystyle MN=CM(a,b)={\frac {2(a^{2}+ab+b^{2})}{3(a+b)}}}$.

L'isobarycentre des quatre sommets du trapèze est, quant à lui, situé au milieu de la médiane. Et le segment découpé sur la parallèle aux bases passant par cet isobarycentre a pour longueur la moyenne arithmétique des deux bases.

Diagonales

En supposant à nouveau que les deux bases a et c sont distinctes^[7], les diagonales p et q sont liées aux quatre côtés par les formules^[4],[8] :

${\displaystyle p^{2}=ac+{\frac {ad^{2}-cb^{2}}{a-c}},\quad q^{2}=ac+{\frac {ab^{2}-cd^{2}}{a-c}}}$,

équivalentes à

${\displaystyle 2ac=p^{2}+q^{2}-b^{2}-d^{2},\quad a(p^{2}-q^{2}+b^{2}-d^{2})=c(p^{2}-q^{2}+d^{2}-b^{2})}$.

Ces deux formules permettent de retrouver les deux bases du trapèze précédent, s'il n'est ni isocèle, ni réduit à un triangle, connaissant les deux autres côtés et les diagonales^[9]. En effet, dans ce cas, les formules sont équivalentes à

${\displaystyle a^{2}={\frac {(p^{2}-b^{2})^{2}-(q^{2}-d^{2})^{2}}{2(p^{2}+b^{2}-q^{2}-d^{2})}},\quad c^{2}={\frac {(p^{2}-d^{2})^{2}-(q^{2}-b^{2})^{2}}{2(p^{2}+d^{2}-q^{2}-b^{2})}}}$.

Le segment découpé par les côtés sur la parallèle aux bases passant par l'intersection des diagonales a pour longueur la moyenne harmonique des deux bases^[10].

Théorème du trapèze

Dans un trapèze, la droite joignant le point d'intersection des côtés non parallèles au point d'intersection des diagonales, passe par les milieux des côtés parallèles.

Plus précisément : soit ABCD un quadrilatère dont les côtés (AD) et (BC) se coupent en P et les diagonales (AC) et (BD) en O, et soient I et J les milieux respectifs de [AB] et [CD]. Alors, le quadrilatère est un trapèze si et seulement si I appartient à (OP) (ou, ce qui est donc équivalent : si J appartient à cette droite). De plus, les quatre points (O, P, I, J) sont alors en division harmonique^[11],[12].

Méthode des trapèzes

La méthode de calcul intégral approché dite « des trapèzes », décrite par Isaac Newton et son élève Roger Cotes, consiste à remplacer les arcs de courbe successifs M_iM_i+1 par les segments [M_iM_i+1] : c'est une interpolation linéaire.

La méthode des trapèzes est plus précise que la méthode élémentaire, dite des rectangles, correspondant aux sommes de Riemann, consistant à remplacer la fonction donnée par une fonction en escalier.

Notes et références

• Portail de la géométrie