Heptadécagone

Cet article est une ébauche concernant la géométrie.
Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.
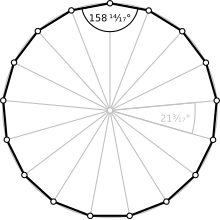
Un heptadécagone est un polygone à 17 sommets, donc 17 côtés et 119 diagonales.
La somme des angles internes d'un heptadécagone non croisé vaut 15π radians, soit 2 700 degrés.
Dans l'heptadécagone régulier convexe, chaque angle interne vaut donc 15π/17 rad, soit environ 158,82°.
Heptadécagones réguliers
Un heptadécagone régulier est un heptadécagone dont les 17 côtés ont la même longueur et dont les angles internes ont même mesure. Il y en a huit : sept étoilés (les heptadécagrammes notés {17/k} pour k de 2 à 8) et un convexe (noté {17}). C'est de ce dernier qu'il s'agit lorsqu'on parle de « l'heptadécagone régulier ».
- Les sept heptadécagones réguliers étoilés
-
 {17/2}
{17/2} -
 {17/3}
{17/3} -
 {17/4}
{17/4} -
 {17/5}
{17/5} -
 {17/6}
{17/6} -
 {17/7}
{17/7} -
 {17/8}
{17/8}
Construction à la règle et au compas

L'annonce de la construction à la règle et au compas de l'heptadécagone régulier a été faite par Carl Friedrich Gauss en 1796, et seulement dans un court article, Neue Entdeckungen, paru au numéro 66, du , de l'Intelligenzblatt der Allgemeinen Literatur-Zeitung de Iéna. Il fallut attendre cinq ans encore, avec la publication de ses Disquisitiones arithmeticae, pour découvrir la substance de cette construction (à l'article « Theorie von grösserem Umfange », en fin d'ouvrage).
Le sinus et le cosinus de l'angle sont respectivement égaux à :
- ;
- .
Par définition, le problème de la construction de l'heptadécagone régulier revient à chercher les racines complexes du polynôme
On note α = 2π/17, puis on pose ω17 = exp(iα), et ωk = ωk
17, pour k entre 1 et 16, qui sont donc les racines recherchées. On va construire des sommes de ces racines à partir de périodes qui forment les racines de polynômes du second degré[1]. On considère le tableau suivant, qui donne la valeur de, pour m entre 0 et 15, de 3m modulo 17 :
{{| |- ! scope="row" | | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |- ! scope="row" | | 1 | 3 | 9 | 10 | 13 | 5 | 15 | 11 | 16 | 14 | 8 | 7 | 4 | 12 | 2 | 6 |- |}}
On utilise la congruence modulo 3 car 3 est une racine primitive de 17.
On pose donc les sommes :
Par les propriétés de symétrie, on peut observer que :
On peut remarquer, par les identités trigonométriques usuelles, que :
Ainsi, X1 et X2 sont les deux racines de X2 + X – 4 = 0, et une étude rapide de signe montre que X1 est la racine positive, et X1 > X2.
De même, on peut montrer que Y1 et Y2 sont les deux racines de Y2 + X1Y – 1 = 0, avec Y1 > Y2, et que Y3 et Y4 sont les deux racines de Y2 + X2Y – 1 = 0, avec Y3 > Y4.
Enfin, on peut vérifier que z1 = 2 cos α = ω1
17 + ω16
17 et z2 = 2 cos 4α = ω4
17 + ω13
17 sont les deux racines de Z2 – Y1Z + Y3 = 0, avec z1 > z2.
Il suffit dès lors de résoudre les équations du second degré et de ne retenir que les racines adéquates pour obtenir le résultat voulu.
On peut déduire des calculs précédents une construction de l'heptadécagone régulier à partir d'un cercle donné de centre O[2]:
- poser A et B sur le cercle tel que
- construire I tel que OI = 1/4OB
- construire E sur [OA] tel que
- construire F sur (OA) tel que
- construire le cercle de diamètre AF, il coupe [OB] en K
- le cercle de centre E et de rayon EK coupe (OA) en N3 et N5, avec N3 sur [OA]
- on construit P3 et P5, les projetés de N3 et N5 sur le cercle d'origine. Ces deux point sont deux sommets de l'heptadécagone, car et
Références
Voir aussi
Sur les autres projets Wikimedia :
- Heptadécagones réguliers, sur Wikimedia Commons
- heptadécagone, sur le Wiktionnaire
- (en) Eric W. Weisstein, « Heptadecagon », sur MathWorld
- (en) Eric W. Weisstein, « Trigonometry Angles — Pi/17 », sur MathWorld
v · m | |||||||
|---|---|---|---|---|---|---|---|
| Triangles | |||||||
| Quadrilatères | |||||||
| Par nombre de côtés |
| ||||||
| Autres classements que par le nombre des côtés |
| ||||||
| Polygones réguliers étoilés |
| ||||||
| Description |
| ||||||
| Droites et cercles remarquables | |||||||
| Relations entre polygones | |||||||
| Construction | |||||||
| Dissection | |||||||
 Portail de la géométrie
Portail de la géométrie























![{\displaystyle {\begin{array}{ccl}X_{1}X_{2}&=&4(\cos \alpha +\cos 8\alpha +\cos 4\alpha +\cos 2\alpha )(\cos 3\alpha +\cos 7\alpha +\cos 5\alpha +\cos 6\alpha )\\&=&4(\cos \alpha \cos 3\alpha +\cos \alpha \cos 7\alpha +\cos \alpha \cos 5\alpha +\cos \alpha \cos 6\alpha \\&&+\cos 8\alpha \cos 3\alpha +\cos 8\alpha \cos 7\alpha +\cos 8\alpha \cos 5\alpha +\cos 8\alpha \cos 6\alpha \\&&+\cos 4\alpha \cos 3\alpha +\cos 4\alpha \cos 7\alpha +\cos 4\alpha \cos 5\alpha +\cos 4\alpha \cos 6\alpha \\&&+\cos 2\alpha \cos 3\alpha +\cos 2\alpha \cos 7\alpha +\cos 2\alpha \cos 5\alpha +\cos 2\alpha \cos 6\alpha )\\&=&2[(\cos 4\alpha +\cos 2\alpha )+(\cos 8\alpha +\cos 6\alpha )+(\cos 6\alpha +\cos 4\alpha )+(\cos 7\alpha +\cos 5\alpha )\\&&+(\cos 11\alpha +\cos 5\alpha )+(\cos 15\alpha +\cos \alpha )+(\cos 13\alpha +\cos 3\alpha )+(\cos 14\alpha +\cos 2\alpha )\\&&+(\cos 7\alpha +\cos \alpha )+(\cos 11\alpha +\cos 3\alpha )+(\cos 9\alpha +\cos \alpha )+(\cos 10\alpha +\cos 2\alpha )\\&&+(\cos 5\alpha +\cos \alpha )+(\cos 9\alpha +\cos 5\alpha )+(\cos 7\alpha +\cos 3\alpha )+(\cos 8\alpha +\cos 4\alpha )]\\&=&2[(\cos 4\alpha +\cos 2\alpha )+(\cos 8\alpha +\cos 6\alpha )+(\cos 6\alpha +\cos 4\alpha )+(\cos 7\alpha +\cos 5\alpha )\\&&+(\cos 6\alpha +\cos 5\alpha )+(\cos 2\alpha +\cos \alpha )+(\cos 4\alpha +\cos 3\alpha )+(\cos 3\alpha +\cos 2\alpha )\\&&+(\cos 7\alpha +\cos \alpha )+(\cos 6\alpha +\cos 3\alpha )+(\cos 8\alpha +\cos \alpha )+(\cos 7\alpha +\cos 2\alpha )\\&&+(\cos 5\alpha +\cos \alpha )+(\cos 6\alpha +\cos 5\alpha )+(\cos 7\alpha +\cos 3\alpha )+(\cos 8\alpha +\cos 4\alpha )]\\&=&8\sum _{k=1}^{8}\cos k\alpha \\&=&-4.\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6909af61f67d3ab308e9052c2685acf7c3db24cb)













