Háromszög

Háromszög
Általános háromszög
Élek, csúcsok száma	3
Átlók száma	0
Belső szögek összege	180°
Szabályos háromszög
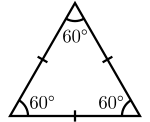szabályos (egyenlő oldalú) háromszög
Schläfli-szimbólum	{3}
Szimmetriacsoport	D3 diédercsoport
Terület: egységnyi oldalra	0,433013
Belső szög	60°

A geometriában a háromszög olyan sokszög, amelynek három oldala, másként fogalmazva három csúcsa van. Egy A, B és C csúcsokkal rendelkező háromszög írásban így is jelölhető: ABC△.

Osztályozás

A háromszögeket csoportokba oszthatjuk oldalaik egymáshoz viszonyított hossza szerint:

• Az általános háromszög minden oldala különböző hosszú, és belső szögei is különbözőek.
• Az egyenlő szárú háromszögnek legalább két oldala azonos hosszúságú. Egyben két belső szöge is ugyanakkora (az alapon fekvfbd
• szabályos háromszög minden oldala azonos hosszúságú. Egyben minden belső szöge is ugyanakkora, mégpedig 60°; szabályos sokszög.^[1]

• 
  Általános háromszög
• 
  Egyenlő szárú háromszög
• 
  Egyenlő oldalú háromszög

A háromszögek csoportosíthatók legnagyobb belső szögük mérete szerint is:

• A derékszögű háromszögnek van egy 90°-os belső szöge (egy derékszög). A derékszöggel szemközti oldalt átfogónak, a derékszöget közrefogó másik két oldalt befogóknak nevezzük.
• A tompaszögű háromszögnek van egy 90°-nál nagyobb belső szöge (egy tompaszög).
• A hegyesszögű háromszögnek mindhárom szöge 90°-nál kisebb (három hegyesszög).

• 
  Derékszögű háromszög
• 
  Tompaszögű háromszög
• 
  Hegyesszögű háromszög

Van két különleges, a geometriában gyakran előforduló derékszögű háromszög. A „45-45-90 háromszögnek” az említett nagyságú szögei vannak, oldalainak aránya: ${\displaystyle 1:1:{\sqrt {2}}}$. A „30-60-90 háromszög” oldalainak aránya ${\displaystyle 1:{\sqrt {3}}:2}$.

• 
  45-45-90 háromszög
• 
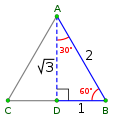  30-60-90 háromszög

Szabályos háromszög

A szabályos háromszögnek vagy egyenlő oldalú háromszögnek minden oldala egyenlő és minden szöge 60°.

Területe ${\displaystyle T={\tfrac {1}{4}}{\sqrt {3}}a^{2}}$, magassága ${\displaystyle m={\tfrac {1}{2}}{\sqrt {3}}a}$, a beírt kör sugara ${\displaystyle r={\tfrac {1}{6}}{\sqrt {3}}a}$, a köré írt kör sugara ${\displaystyle R={\tfrac {1}{3}}{\sqrt {3}}a}$.

Elemi tények

A háromszögekre vonatkozó alapvető tényeket már Euklidesz lefektette Elemek c. művének 1-4. könyvében Kr. e. 300 körül. A háromszög egy sokszög, és egy 2-simplex (lásd politóp). Minden háromszög kétdimenziós.

Egy háromszögben nagyobb oldallal szemben nagyobb szög van; azaz: ha hosszúság szerinti sorrendbe állítjuk az oldalakat, pl. a≤b≤c, akkor a megfelelő (az oldalakkal szemközti) szögek is ugyanilyen nagyság szerinti sorrendben követik egymást, α≤β≤γ; és fordítva: ha a szögeket állítjuk ilyen sorrendbe, akkor a megfelelő oldalak is ugyanilyen sorrendben fogják egymást követni. Ehhez hasonló állítást emlegetnek néha olló-tétel néven: ha két háromszögben két-két oldal páronként egyenlő, és az általuk közrefogott szög kisebb az elsőben, mint a másodikban, akkor a harmadik oldal is kisebb az elsőben, mint a másodikban.

Két háromszög akkor és csak akkor hasonló, ha létezik olyan megfeleltetés, ahol a szögeik megegyeznek. Ebben az esetben megfelelő oldalaik aránya is megegyezik. Ebből következően két háromszög hasonló, hogyha létezik olyan megfeleltetés, amelyben:

1. két megfelelő szögük megegyezik,
2. két megfelelő oldal aránya és a közbezárt szög megegyezik,
3. megfelelő oldalaik aránya megegyezik,
4. két megfelelő oldal aránya, és a nagyobbikkal szemközti szög megegyezik

Derékszögű háromszögeket és a hasonlóság fogalmát felhasználva definiálhatjuk a szinusz és koszinusz trigonometriai függvényeket.

Az euklideszi geometriában a háromszög belső szögeinek összege (α + β + γ) megegyezik a derékszög kétszeresével (180° vagy π radián). Ebből következik, hogy a háromszög két szögének ismeretében meg lehet határozni a harmadikat. (Nemeuklideszi geometriáknál nem áll fenn az egyenlőség: ha a geometria hiperbolikus, akkor a háromszög szögeinek összege kisebb mint 180°.)

Egy fontos tétel a Pitagorasz-tétel, ami kimondja, hogy bármely derékszögű háromszögben az átfogó négyzete megegyezik a két befogó négyzetének összegével. Ha c az átfogó, a tétel az alábbi alakban írható le:

${\displaystyle c^{2}=a^{2}+b^{2}\,}$

Ami azt is jelenti, hogy a derékszögű háromszög bármelyik két oldalából meg lehet határozni a harmadik oldalt. A Pitagorasz-tétel általánosítása a koszinusztétel:

${\displaystyle c^{2}=a^{2}+b^{2}-2ab\cos \gamma \,}$

ami minden háromszögre igaz, nem csak abban az esetben, ahol γ derékszögű. A koszinusztétel lehetővé teszi a háromszög szögeinek és oldalainak meghatározását, ha ismert a háromszög három oldala, vagy két oldal és az általuk közrefogott szög.

A szinusztétel kimondja, hogy bármely háromszögben, egy oldal hosszának és az oldallal szemközti szög szinuszának a hányadosa független az oldal választásától, a hányados pedig egyenlő a köré írt kör átmérőjével:

${\displaystyle {\frac {a}{\sin \alpha }}={\frac {b}{\sin \beta }}={\frac {c}{\sin \gamma }}=2R}$

ahol R a körülírt kör (a mindhárom csúcson áthaladó kör) sugara. A szinusztételt fel lehet használni a háromszög oldalainak meghatározására két szög és egy oldal ismeretében. Ha két oldal és egy nem meghatározott helyű szög adott, a szinusztétel akkor is használható; ebben az esetben 0, 1 vagy 2 megoldás lehetséges.

Magasság és terület

A háromszög magassága a háromszög csúcsa és a szemközti oldalegyenes távolsága. A háromszög magasságvonalai egy pontban, a magasságpontban metszik egymást.

Az a, b és c oldalakhoz tartozó magasságokat m_a, m_b és m_c szimbólumokkal jelölik, és a következőképpen számíthatóak ki:

m_a=b sinγ=c sinβ

m_b=a sinγ=c sinα

m_c=a sinβ=b sinα

A terület valamely oldal és a hozzá tartozó magasság ismeretében számítható:

${\displaystyle T={\frac {am_{a}}{2}}={\frac {ab\sin \gamma }{2}}={\frac {ac\sin \beta }{2}}}$

${\displaystyle T={\frac {bm_{b}}{2}}={\frac {ba\sin \gamma }{2}}={\frac {bc\sin \alpha }{2}}}$

${\displaystyle T={\frac {cm_{c}}{2}}={\frac {ca\sin \beta }{2}}={\frac {cb\sin \alpha }{2}}}$

Kiszámítható csak az oldalak ismeretében is (Hérón-képlet):

${\displaystyle T={\sqrt {s(s-a)(s-b)(s-c)}}}$, ahol ${\displaystyle s={\frac {a+b+c}{2}}}$ a félkerület.

A szabályos háromszög esetében a képlet a következőképpen egyszerűsödik le:

${\displaystyle T={\frac {am_{a}}{2}}={\frac {a^{2}\sin 60^{\circ }}{2}}={\frac {a^{2}{\sqrt {3}}}{4}}}$

A háromszöghöz kapcsolódó nevezetes pontok, egyenesek és körök

A háromszögnek több száz, bizonyos szempontból egyedi pontját meg lehet szerkeszteni: a külső hivatkozások között megtalálható ezek katalógusa. Ezek a pontok gyakran három, a csúcsokkal valamilyen szimmetriát mutató egyenes közös metszéspontjai: a közös metszéspont létezésének bizonyításához használható segédeszköz például a Ceva-tétel. Hasonlóan, a háromszög nevezetes egyeneseit gyakran három, valamilyen szimmetriát felhasználva megszerkesztett pont határozza meg, amelyek egy egyenesbe esnek: itt például a Menelaosz-tétel segítségével lehet bizonyítani az egyenes létezését.

A háromszög felező merőlegesei olyan egyenesek, amik átmennek egy oldal felezőpontján és merőlegesek az oldalra. A három felező merőleges egy pontban találkozik, a háromszög köréírt körének középpontjában. A köréírt kör sugara a fentebb említett szinusztételben lévő R, ebből adódik rá a képlet:

${\displaystyle R={\frac {a}{2\sin \alpha }}={\frac {b}{2\sin \beta }}={\frac {c}{2\sin \gamma }}}$

Tovább egyszerűsödik a formula a szabályos háromszög esetében:

${\displaystyle R={\frac {a}{2\sin(60^{\circ })}}={\frac {a}{\sqrt {3}}}={\frac {a{\sqrt {3}}}{3}}}$

A Thalész-tétel kimondja, hogy ha a háromszög köré írt kör középpontja valamelyik oldalon van rajta, akkor a szemközti szög derékszög. Ennél többet is tudunk: ha a középpont a háromszög belsejében van, a háromszög hegyesszögű, ha kívül van a háromszögön, akkor a háromszög tompaszögű.

A háromszög magasságvonalán a csúcspontot a szemközti oldallal derékszögben összekötő vonalat értjük. Ezt a szemközti oldalt a magasság alapjának, a magasságvonal és az alap metszéspontját a magasság talppontjának nevezzük. A magasságvonal hossza a csúcspont és az alap közötti távolsággal egyenlő. A három magasságvonal egy pontban metszi egymást, a háromszög magasságpontjában. A magasságpont akkor és csak akkor van a háromszög belsejében, ha a háromszög nem tompaszögű. A három csúcspont és a magasságpont olyan ortocentrikus pontnégyest alkotnak, melyben bármelyik három pontból alkotott háromszög magasságpontja éppen a negyedik pont.

A háromszög szögfelezője az a csúcson átmenő egyenes, ami a csúcshoz tartozó szöget kettéosztja. A szögfelező minden pontja a szög melletti oldalaktól egyenlő távolságra van. A három szögfelező egy pontban metszi egymást, a beírt kör középpontjában. A beírt kör a háromszög belsejében található kör, ami mindhárom oldalt belülről érinti. Sugarára a szabályos háromszög esetében van egyszerű képlet: ${\displaystyle r={\tfrac {1}{6}}{\sqrt {3}}a}$. A külső szögfelezők metszéspontjaiban találhatók másik három fontos kör, a háromszög hozzáírt köreinek a középpontja. A hozzáírt körök a háromszögön kívül helyezkednek el, egy-egy oldalt, és a másik két oldal meghosszabbításait érintik. A hozzáírt körök középpontjai a beírt kör középpontjával olyan ortocentrikus pontnégyest alkotnak, melyben bármelyik három pontból alkotott háromszög magasságpontja éppen a negyedik pont. Mivel a beírt kör és a három hozzáírt kör mindegyike mindhárom oldalt érinti, ezért a négy kört néha tritangens köröknek is szokták nevezni.

A háromszög súlyvonala egy csúcspont és a szemközti oldal felezőpontját összekötő szakasz, ami a háromszöget két egyenlő területű részre bontja. A három súlyvonal egy pontban metszi egymást, a metszéspontot a háromszög súlypontjának nevezzük. A súlypont egyben a háromszög tömegközéppontja is: ha a háromszöget például fából legyártanánk, a súlypontot vagy az egész súlyvonalat alátámasztva egyensúlyban lenne. A súlypont 2:1 arányban osztja a súlyvonalat úgy, hogy a csúcstól fekszik távolabb.

A háromszög oldalfelező pontjai és a háromszög magasságainak talppontjai mind egy körön fekszenek, a háromszög Feuerbach-körén vagy a „kilenc pont körén”. A maradék három pontot a magasságpontot a csúcsokkal összekötő szakaszok felezőpontjai adják.

A Feuerbach-kör sugara éppen a fele a körülírt kör sugarának. Érinti a beírt kört a Feuerbach-pontban, és a három hozzáírt kört.

A súlypont (sárga), magasságpont (kék), a körülírt kör középpontja (zöld) és a Feuerbach-kör középpontja (vörös pont) egy egyenesbe esnek, amit Euler-egyenesnek (vörös színnel) neveznek. A Feuerbach-kör középpontja felezi, a súlypont pedig 1:2 arányban osztja a körülírt kör középpontját és a magasságpontot összekötő szakaszt.

A beírt kör középpontja általában nincs az Euler-egyenesen.

Jegyzetek

Források

• Weisstein, Eric W.: A háromszög területe (angol nyelven). Wolfram MathWorld

További információk

• Kiss György: Amit jó tudni a háromszögekről
• Triangle Calculator – solves for remaining sides and angles when given three sides or angles, supports degrees and radians.
• Napoleon's theorem A triangle with three equilateral triangles. A purely geometric proof. It uses the Fermat point to prove Napoleon's theorem without transformations by Antonio Gutiérrez from "Geometry Step by Step from the Land of the Incas"
• William Kahan: Miscalculating Area and Angles of a Needle-like Triangle Archiválva 2006. november 10-i dátummal a Wayback Machine-ben.
• Clark Kimberling: Encyclopedia of triangle centers. Lists some 1600 interesting points associated with any triangle.
• Christian Obrecht: Eukleides. Software package for creating illustrations of facts about triangles and other theorems in Euclidean geometry.
• Triangle constructions, remarkable points and lines, and metric relations in a triangle at cut-the-knot
• Printable Worksheet on Types of Triangles
• Compendium Geometry Analytical Geometry of Triangles