Hérón-képlet

A geometriában a Hérón-képlet a háromszög területét adja meg a háromszög oldalainak függvényében:

T = s ( s − a ) ( s − b ) ( s − c ) {\displaystyle T={\sqrt {s(s-a)(s-b)(s-c)}}}
s = a + b + c 2 {\displaystyle s={\frac {a+b+c}{2}}\,}

ahol a, b és c a háromszög oldalai, s a háromszög kerületének a fele, és T a háromszög területe.

A képletet az alexandriai Hérón vezette be.

Bizonyítás

Elemi

Teljesen elemi (a Pitagorasz-tételre és nevezetes azonosságokra épülő) bizonyítása történhet az általános magasságtétel segítségével.

Trigonometriai

A trigonometriai jellegű bizonyításhoz induljunk ki a koszinusztételből:

cos ⁡ γ = a 2 + b 2 − c 2 2 a b {\displaystyle \cos \gamma ={\frac {a^{2}+b^{2}-c^{2}}{2ab}}}

illetve abból a képletből, amely a háromszög területét két oldal és a közrezárt szög segítségével fejezi ki:

T {\displaystyle T\,} = 1 2 a b sin ⁡ γ {\displaystyle ={\frac {1}{2}}ab\sin \gamma \,}
= 1 2 a b 1 − cos 2 ⁡ γ {\displaystyle ={\frac {1}{2}}ab{\sqrt {1-\cos ^{2}\gamma }}\,}
= 1 2 a b ( 1 − cos ⁡ γ ) ( 1 + cos ⁡ γ ) {\displaystyle ={\frac {1}{2}}ab{\sqrt {(1-\cos \gamma )(1+\cos \gamma )}}\,}
= 1 2 a b ( 1 − c 2 − a 2 − b 2 2 a b ) ( 1 + c 2 − a 2 − b 2 2 a b ) {\displaystyle ={\frac {1}{2}}ab{\sqrt {\left(1-{\frac {c^{2}-a^{2}-b^{2}}{2ab}}\right)\left(1+{\frac {c^{2}-a^{2}-b^{2}}{2ab}}\right)}}}
= 1 4 ( ( a + b ) 2 − c 2 ) ( c 2 − ( a − b ) 2 ) {\displaystyle ={\frac {1}{4}}{\sqrt {\left((a+b)^{2}-c^{2}\right)\left(c^{2}-(a-b)^{2}\right)}}}
= 1 4 ( a + b + c ) ( a + b − c ) ( − a + b + c ) ( a − b + c ) {\displaystyle ={\frac {1}{4}}{\sqrt {(a+b+c)(a+b-c)(-a+b+c)(a-b+c)}}\,}

Ha a fenti képletbe behelyettesítjük a értékét, vagyis

a = 2 s − b − c {\displaystyle a=2s-b-c\,}

akkor pont a Hérón-képletet kapjuk.

Geometriai

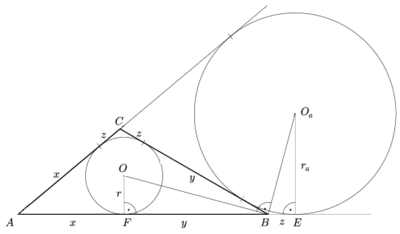Hasonló háromszögek
Hasonló háromszögek

Elég annyit belátni, hogy

  • t = r s = r a ( s − a ) {\displaystyle t=rs=r_{a}(s-a)}
  • r r a = ( s − b ) ( s − c ) {\displaystyle rr_{a}=(s-b)(s-c)}

mert ebből már következik, hogy

t 2 = r s r a ( s − a ) = s ( s − a ) ( s − b ) ( s − c ) . {\displaystyle t^{2}=rsr_{a}(s-a)=s(s-a)(s-b)(s-c).}

Az ábráról leolvasható, hogy

t = t A O B + t B O C + t C O A = a r + b r + c r 2 = r s , {\displaystyle t=t_{AOB}+t_{BOC}+t_{COA}={\frac {ar+br+cr}{2}}=rs,}

és

t = t A O a B + t A O a C − t B O a C = b r a + c r a − a r a 2 = r a ( s − a ) , {\displaystyle t=t_{AO_{a}B}+t_{AO_{a}C}-t_{BO_{a}C}={\frac {br_{a}+cr_{a}-ar_{a}}{2}}=r_{a}(s-a),}

valamint az F O B {\displaystyle FOB} és E B O a {\displaystyle EBO_{a}} derékszögű háromszögek hasonlók.

Könnyen igazolható, hogy F B = y = s − b {\displaystyle FB=y=s-b} és B E = z = s − c {\displaystyle BE=z=s-c} , tehát r s − b = O F F B = B E O a E = s − c r a . {\displaystyle {\frac {r}{s-b}}={\frac {OF}{FB}}={\frac {BE}{O_{a}E}}={\frac {s-c}{r_{a}}}.} A tétel általánosítása gömbháromszögekre vonatkozóan a l'Huillier-tétel.

Más Hérón-képletek

A következőket szintén szokták Hérón-képletnek nevezni:

A húrnégyszög területe

T = ( s − a ) ( s − b ) ( s − c ) ( s − d ) {\displaystyle T={\sqrt {(s-a)(s-b)(s-c)(s-d)}}} ,

ahol s = a + b + c + d 2 {\displaystyle s={\frac {a+b+c+d}{2}}\,} .

Az általános konvex négyszög területe

T = ( s − a ) ( s − b ) ( s − c ) ( s − d ) − a b c d cos 2 ⁡ φ {\displaystyle T={\sqrt {(s-a)(s-b)(s-c)(s-d)-abcd\cos ^{2}\varphi }}} ,

ahol s, mint előbb, φ = α + γ 2 {\displaystyle \varphi ={\frac {\alpha +\gamma }{2}}\,} , és α és γ a négyszög két szemben fekvő szöge.

Az egyenlő oldalú tetraéder térfogata:

V = 1 3 s 2 ( s 2 − a 2 ) ( s 2 − b 2 ) ( s 2 − c 2 ) {\displaystyle V={\frac {1}{3}}{\sqrt {s^{2}(s^{2}-a^{2})(s^{2}-b^{2})(s^{2}-c^{2})}}}

ahol a, b, c a tetraéder egy lapjának oldalhosszai, és s 2 = a 2 + b 2 + c 2 2 {\displaystyle s^{2}={\frac {a^{2}+b^{2}+c^{2}}{2}}\,} .

Kapcsolódó szócikkek

  • Brahmagupta indiai matematikus

Források

  • A Matematika Tanítása 2001. 5. szám
  • (angolul) Eric W. Weisstein, "Heron's Formula." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/HeronsFormula.html