Driehoek (meetkunde)

Een driehoek is een meetkundige figuur die bestaat uit drie punten die niet op een rechte lijn liggen, en de lijnstukken die die punten met elkaar verbinden. De lijnstukken heten de zijden van de driehoek; de punten zijn de hoekpunten van de driehoek. De driehoek met de hoekpunten ${\displaystyle A}$, ${\displaystyle B}$ en ${\displaystyle C}$ wordt genoteerd als ${\displaystyle \triangle ABC}$. Meestal worden voor een willekeurige driehoek de hoekpunten zo gekozen als in de figuur: links het hoekpunt ${\displaystyle A}$, rechts ${\displaystyle B}$ en in de top ${\displaystyle C}$. De grootte van de hoeken van de driehoek wordt meestal overeenkomstig de hoekpunten aangeduid met ${\displaystyle \alpha }$, ${\displaystyle \beta }$ en ${\displaystyle \gamma }$, en de zijden van de driehoek met de letters ${\displaystyle a}$, ${\displaystyle b}$ en ${\displaystyle c}$, zodat ${\displaystyle a}$ de tegenover ${\displaystyle A}$ liggende zijde is, ${\displaystyle b}$ tegenover ${\displaystyle B}$ ligt en ${\displaystyle c}$ tegenover ${\displaystyle C}$.

Een driehoek is een 2-simplex.

Driehoeken liggen aan de basis van de driehoeksmeting, die in de geodesie algemeen wordt gebruikt.

Som van de hoeken

Pythagoras bewees dat de som van de hoeken van een driehoek steeds 180 graden is, al denkt men dat de ontdekking door een van zijn leerlingen is gedaan, maar toch aan hem is toegeschreven.^[bron?]

${\displaystyle \alpha +\beta +\gamma =180^{\circ }}$

Indeling

Er zijn verschillende soorten driehoeken.

Indeling op basis van de hoeken

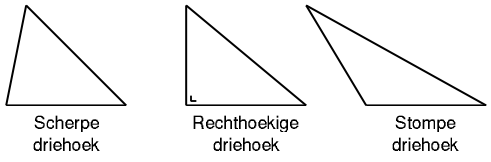
• scherpe (scherphoekige) driehoek: alle hoeken zijn kleiner dan 90 graden.
• rechthoekige driehoek: een van de hoeken is 90 graden.
• stompe (stomphoekige) driehoek: een van de hoeken is groter dan 90 graden.

Indeling op basis van de zijden

Speciale gevallen

• gelijkbenige driehoek: er zijn twee of drie even lange zijden. In het laatste geval is de driehoek gelijkzijdig, iedere gelijkzijdige driehoek is ook gelijkbenig. De beide hoeken die aan de derde zijde grenzen (de basishoeken) zijn aan elkaar gelijk.
• gelijkzijdige driehoek: alle zijden zijn even lang. De drie hoeken zijn ook even groot, namelijk 60°. Verder is vanuit ieder hoekpunt de zwaartelijn tevens de bissectrice en de hoogtelijn. Daarnaast ontstaat er door zes gelijkzijdige driehoeken in elkaar te schuiven een regelmatige zeshoek. Een gelijkzijdige driehoek is een voorbeeld van een regelmatige veelhoek. De oppervlakte ${\displaystyle O}$ van een gelijkzijdige driehoek met zijden van ${\displaystyle z}$ is

${\displaystyle O={\tfrac {1}{4}}{\sqrt {3}}\cdot z^{2}}$

De straal van de omgeschreven cirkel is

${\displaystyle R={\tfrac {1}{3}}a{\sqrt {3}}}$

Ontaarde driehoek

Als de drie hoekpunten op één lijn liggen, is er geen sprake van een echte driehoek. Een van de hoeken is dan 180 graden, de andere twee hoeken zijn 0 graden. Omdat het toch zinvol kan zijn over zo'n driehoek te spreken, wordt die driehoek ontaard genoemd.

Oppervlakte

De oppervlakte O van een driehoek is gelijk aan het halve product van de lengte van een zijde en de lengte van de hoogtelijn op die zijde. Anders geformuleerd: oppervlakte = basis × halve hoogte.

${\displaystyle O={\tfrac {1}{2}}bh_{b}={\tfrac {1}{2}}ab\sin \gamma .}$

Een andere manier om de oppervlakte te berekenen is met de formule van Heron.

${\displaystyle O={\sqrt {s\left(s-a\right)\left(s-b\right)\left(s-c\right)}}}$

Hierin is ${\displaystyle O}$ de oppervlakte van de driehoek, ${\displaystyle a,b}$ en ${\displaystyle c}$ de lengtes van de zijden en ${\displaystyle s}$ de halve omtrek:

${\displaystyle s={\tfrac {1}{2}}(a+b+c)}$.

Deze formule kan omgewerkt worden tot;

${\displaystyle O={\tfrac {1}{4}}{\sqrt {(a^{2}+b^{2}+c^{2})^{2}-2(a^{4}+b^{4}+c^{4})}}}$,

of nog anders geschreven:

${\displaystyle O={\tfrac {1}{4}}{\sqrt {2(a^{2}b^{2}+b^{2}c^{2}+a^{2}c^{2})-(a^{4}+b^{4}+c^{4})}}}$.

3D

Driehoeken vormen de basis voor 3D-berekeningen met polygonen.

Vakwerk

Een driehoek met scharnierende hoekpunten is de eenvoudigste statisch bepaalde constructie die met balken kan worden gemaakt (zie Stabiliteitsverband). Driehoeken vormen de basis van zogenaamde vakwerkconstructies, wat goed te zien is in huizen die geconstrueerd zijn op basis van vakwerkbouw. Ook grote staalskeletbouwsels zoals hijskranen maken hiervan gebruik.

Meetkundige begrippen met betrekking tot driehoeken

• bissectrice
• driehoekscentrum, voor speciale meetkundige punten in een driehoek
• hoek
• hoogtelijn
• orthologie
• stelling van Pythagoras
• zwaartelijn

Zie de categorie Triangles van Wikimedia Commons voor mediabestanden over dit onderwerp.