Parabolic coordinates

In green, confocal parabolae opening upwards, 2 y = x 2 σ 2 − σ 2 {\displaystyle 2y={\frac {x^{2}}{\sigma ^{2}}}-\sigma ^{2}} In red, confocal parabolae opening downwards, 2 y = − x 2 τ 2 + τ 2 {\displaystyle 2y=-{\frac {x^{2}}{\tau ^{2}}}+\tau ^{2}}

Parabolic coordinates are a two-dimensional orthogonal coordinate system in which the coordinate lines are confocal parabolas. A three-dimensional version of parabolic coordinates is obtained by rotating the two-dimensional system about the symmetry axis of the parabolas.

Parabolic coordinates have found many applications, e.g., the treatment of the Stark effect and the potential theory of the edges.

Two-dimensional parabolic coordinates

Two-dimensional parabolic coordinates ( σ , τ ) {\displaystyle (\sigma ,\tau )} are defined by the equations, in terms of Cartesian coordinates:

x = σ τ {\displaystyle x=\sigma \tau }
y = 1 2 ( τ 2 − σ 2 ) {\displaystyle y={\frac {1}{2}}\left(\tau ^{2}-\sigma ^{2}\right)}

The curves of constant σ {\displaystyle \sigma } form confocal parabolae

2 y = x 2 σ 2 − σ 2 {\displaystyle 2y={\frac {x^{2}}{\sigma ^{2}}}-\sigma ^{2}}

that open upwards (i.e., towards + y {\displaystyle +y} ), whereas the curves of constant τ {\displaystyle \tau } form confocal parabolae

2 y = − x 2 τ 2 + τ 2 {\displaystyle 2y=-{\frac {x^{2}}{\tau ^{2}}}+\tau ^{2}}

that open downwards (i.e., towards − y {\displaystyle -y} ). The foci of all these parabolae are located at the origin.

The Cartesian coordinates x {\displaystyle x} and y {\displaystyle y} can be converted to parabolic coordinates by:

σ = sign ⁡ ( x ) x 2 + y 2 − y {\displaystyle \sigma =\operatorname {sign} (x){\sqrt {{\sqrt {x^{2}+y^{2}}}-y}}}
τ = x 2 + y 2 + y {\displaystyle \tau ={\sqrt {{\sqrt {x^{2}+y^{2}}}+y}}}

Two-dimensional scale factors

The scale factors for the parabolic coordinates ( σ , τ ) {\displaystyle (\sigma ,\tau )} are equal

h σ = h τ = σ 2 + τ 2 {\displaystyle h_{\sigma }=h_{\tau }={\sqrt {\sigma ^{2}+\tau ^{2}}}}

Hence, the infinitesimal element of area is

d A = ( σ 2 + τ 2 ) d σ d τ {\displaystyle dA=\left(\sigma ^{2}+\tau ^{2}\right)d\sigma d\tau }

and the Laplacian equals

∇ 2 Φ = 1 σ 2 + τ 2 ( ∂ 2 Φ ∂ σ 2 + ∂ 2 Φ ∂ τ 2 ) {\displaystyle \nabla ^{2}\Phi ={\frac {1}{\sigma ^{2}+\tau ^{2}}}\left({\frac {\partial ^{2}\Phi }{\partial \sigma ^{2}}}+{\frac {\partial ^{2}\Phi }{\partial \tau ^{2}}}\right)}

Other differential operators such as ∇ ⋅ F {\displaystyle \nabla \cdot \mathbf {F} } and ∇ × F {\displaystyle \nabla \times \mathbf {F} } can be expressed in the coordinates ( σ , τ ) {\displaystyle (\sigma ,\tau )} by substituting the scale factors into the general formulae found in orthogonal coordinates.

Three-dimensional parabolic coordinates

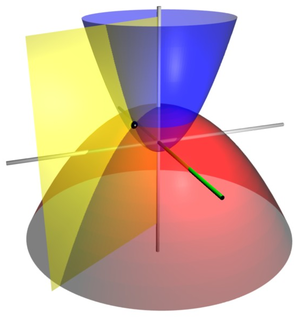
Coordinate surfaces of the three-dimensional parabolic coordinates. The red paraboloid corresponds to τ=2, the blue paraboloid corresponds to σ=1, and the yellow half-plane corresponds to φ=-60°. The three surfaces intersect at the point P (shown as a black sphere) with Cartesian coordinates roughly (1.0, -1.732, 1.5).

The two-dimensional parabolic coordinates form the basis for two sets of three-dimensional orthogonal coordinates. The parabolic cylindrical coordinates are produced by projecting in the z {\displaystyle z} -direction. Rotation about the symmetry axis of the parabolae produces a set of confocal paraboloids, the coordinate system of tridimensional parabolic coordinates. Expressed in terms of cartesian coordinates:

x = σ τ cos ⁡ φ {\displaystyle x=\sigma \tau \cos \varphi }
y = σ τ sin ⁡ φ {\displaystyle y=\sigma \tau \sin \varphi }
z = 1 2 ( τ 2 − σ 2 ) {\displaystyle z={\frac {1}{2}}\left(\tau ^{2}-\sigma ^{2}\right)}

where the parabolae are now aligned with the z {\displaystyle z} -axis, about which the rotation was carried out. Hence, the azimuthal angle φ {\displaystyle \varphi } is defined

tan ⁡ φ = y x {\displaystyle \tan \varphi ={\frac {y}{x}}}

The surfaces of constant σ {\displaystyle \sigma } form confocal paraboloids

2 z = x 2 + y 2 σ 2 − σ 2 {\displaystyle 2z={\frac {x^{2}+y^{2}}{\sigma ^{2}}}-\sigma ^{2}}

that open upwards (i.e., towards + z {\displaystyle +z} ) whereas the surfaces of constant τ {\displaystyle \tau } form confocal paraboloids

2 z = − x 2 + y 2 τ 2 + τ 2 {\displaystyle 2z=-{\frac {x^{2}+y^{2}}{\tau ^{2}}}+\tau ^{2}}

that open downwards (i.e., towards − z {\displaystyle -z} ). The foci of all these paraboloids are located at the origin.

The Riemannian metric tensor associated with this coordinate system is

g i j = [ σ 2 + τ 2 0 0 0 σ 2 + τ 2 0 0 0 σ 2 τ 2 ] {\displaystyle g_{ij}={\begin{bmatrix}\sigma ^{2}+\tau ^{2}&0&0\\0&\sigma ^{2}+\tau ^{2}&0\\0&0&\sigma ^{2}\tau ^{2}\end{bmatrix}}}

Three-dimensional scale factors

The three dimensional scale factors are:

h σ = σ 2 + τ 2 {\displaystyle h_{\sigma }={\sqrt {\sigma ^{2}+\tau ^{2}}}}
h τ = σ 2 + τ 2 {\displaystyle h_{\tau }={\sqrt {\sigma ^{2}+\tau ^{2}}}}
h φ = σ τ {\displaystyle h_{\varphi }=\sigma \tau }

It is seen that the scale factors h σ {\displaystyle h_{\sigma }} and h τ {\displaystyle h_{\tau }} are the same as in the two-dimensional case. The infinitesimal volume element is then

d V = h σ h τ h φ d σ d τ d φ = σ τ ( σ 2 + τ 2 ) d σ d τ d φ {\displaystyle dV=h_{\sigma }h_{\tau }h_{\varphi }\,d\sigma \,d\tau \,d\varphi =\sigma \tau \left(\sigma ^{2}+\tau ^{2}\right)\,d\sigma \,d\tau \,d\varphi }

and the Laplacian is given by

∇ 2 Φ = 1 σ 2 + τ 2 [ 1 σ ∂ ∂ σ ( σ ∂ Φ ∂ σ ) + 1 τ ∂ ∂ τ ( τ ∂ Φ ∂ τ ) ] + 1 σ 2 τ 2 ∂ 2 Φ ∂ φ 2 {\displaystyle \nabla ^{2}\Phi ={\frac {1}{\sigma ^{2}+\tau ^{2}}}\left[{\frac {1}{\sigma }}{\frac {\partial }{\partial \sigma }}\left(\sigma {\frac {\partial \Phi }{\partial \sigma }}\right)+{\frac {1}{\tau }}{\frac {\partial }{\partial \tau }}\left(\tau {\frac {\partial \Phi }{\partial \tau }}\right)\right]+{\frac {1}{\sigma ^{2}\tau ^{2}}}{\frac {\partial ^{2}\Phi }{\partial \varphi ^{2}}}}

Other differential operators such as ∇ ⋅ F {\displaystyle \nabla \cdot \mathbf {F} } and ∇ × F {\displaystyle \nabla \times \mathbf {F} } can be expressed in the coordinates ( σ , τ , ϕ ) {\displaystyle (\sigma ,\tau ,\phi )} by substituting the scale factors into the general formulae found in orthogonal coordinates.

See also

Bibliography

  • Morse PM, Feshbach H (1953). Methods of Theoretical Physics, Part I. New York: McGraw-Hill. p. 660. ISBN 0-07-043316-X. LCCN 52011515.
  • Margenau H, Murphy GM (1956). The Mathematics of Physics and Chemistry. New York: D. van Nostrand. pp. 185–186. LCCN 55010911.
  • Korn GA, Korn TM (1961). Mathematical Handbook for Scientists and Engineers. New York: McGraw-Hill. p. 180. LCCN 59014456. ASIN B0000CKZX7.
  • Sauer R, Szabó I (1967). Mathematische Hilfsmittel des Ingenieurs. New York: Springer Verlag. p. 96. LCCN 67025285.
  • Zwillinger D (1992). Handbook of Integration. Boston, MA: Jones and Bartlett. p. 114. ISBN 0-86720-293-9. Same as Morse & Feshbach (1953), substituting uk for ξk.
  • Moon P, Spencer DE (1988). "Parabolic Coordinates (μ, ν, ψ)". Field Theory Handbook, Including Coordinate Systems, Differential Equations, and Their Solutions (corrected 2nd ed., 3rd print ed.). New York: Springer-Verlag. pp. 34–36 (Table 1.08). ISBN 978-0-387-18430-2.

External links