Distribució de Poisson

Infotaula distribució de probabilitat Distribució de Poisson
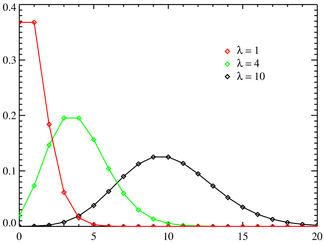Plot of the Poisson PMF
L'eix horitzontal és l'índex k . La funció només està definida en valors sencers de k . Les línies que connecten els punts són només guies per a l'ull i no indiquen continuïtat.
Funció de distribució de probabilitat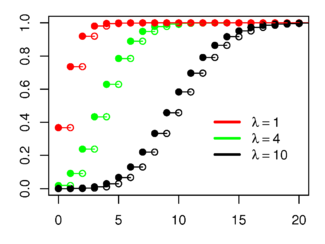
Plot of the Poisson CDF
L'eix horitzontal és l'índex k .
Tipusdistribution de Tweedie, distribució binomial, natural exponential family with quadratic variance function (en) Tradueix, Distribució de Conway–Maxwell–Poisson, Panjer distribution (en) Tradueix, Distribució de Poisson composta, distribució univariant i distribució de probabilitat discreta Modifica el valor a Wikidata
EpònimSiméon Denis Poisson Modifica el valor a Wikidata
Paràmetres λ ∈ ( 0 , ∞ ) {\displaystyle \lambda \in (0,\infty )}
Suportk ∈ { 0, 1, 2, 3, ... }
FD Γ ( ⌊ k + 1 ⌋ , λ ) ⌊ k ⌋ ! per  k ≥ 0 {\displaystyle {\frac {\Gamma (\lfloor k+1\rfloor ,\lambda )}{\lfloor k\rfloor !}}{\text{per }}k\geq 0} (on Γ ( x , y ) {\displaystyle \Gamma (x,y)} és la Funció gamma incompleta)
Esperança matemàtica λ {\displaystyle \lambda \,}
Mediana normalment prop de ⌊ λ + 1 / 3 − 002 / λ ⌋ {\displaystyle {\text{normalment prop de}}\lfloor \lambda +1/3-002/\lambda \rfloor }
Moda ⌊ λ ⌋ (amb  λ − 1  si  λ  és un enter) {\displaystyle \lfloor \lambda \rfloor {\text{(amb }}\lambda -1{\text{ si }}\lambda {\text{ és un enter)}}}
Variància λ {\displaystyle \lambda \,}
Coeficient de simetria λ − 1 / 2 {\displaystyle \lambda ^{-1/2}\,}
Curtosi 3 + λ − 1 {\displaystyle 3+\lambda ^{-1}\,}
Entropia λ [ 1 − ln ⁡ ( λ ) ] + i − λ ∑ k = 0 ∞ λ k ln ⁡ ( k ! ) k ! {\displaystyle \lambda [1\!-\!\ln(\lambda )]\!+\!i^{-\lambda }\sum _{k=0}^{\infty }{\frac {\lambda ^{k}\ln(k!)}{k!}}}
FC exp ⁡ ( λ ( e i t − 1 ) ) {\displaystyle \exp(\lambda (e^{it}-1))\,}
EOMPoisson_distribution Modifica el valor a Wikidata
MathworldPoissonDistribution Modifica el valor a Wikidata

En teoria de probabilitat i estadística, la distribució de Poisson o llei dels petits nombres o dels fenòmens rars és una distribució de probabilitat discreta que és un bon model per molts fenòmens naturals o socials. Una propietat especialment important és que una distribució binomial de paràmetres n {\displaystyle n} i p {\displaystyle p} , B ( n , p ) {\displaystyle B(n,p)} , amb n {\displaystyle n} gran i p {\displaystyle p} petitat es pot aproximar (en distribució) per una distribució de Poisson de paràmetre n × p {\displaystyle n\times p} ; moltes de les aplicacions de la distribució de Poisson es justifiquen en base aquesta propietat.

Aquesta distribució va ser introduïda per Siméon-Denis Poisson l'any 1837 en el seu treball Recherches sur la probabilité des jugements en matière criminelle et en matière civile[1] ( Investigació sobre la probabilitat dels judicis en matèries criminals i civils ).


Les referències bàsiques d'aquesta pàgina són[2][3]

Definició

Una variable aleatòria de Poisson X {\displaystyle X} de paràmetre λ > 0 {\displaystyle \lambda >0} és una variable discreta que pot prendre qualsevol valor natural, 0, 1, 2, ... amb probabilitats

P ( X = k ) = e − λ λ k k ! ,   k = 0 , 1 , 2 , … {\displaystyle P(X=k)=e^{-\lambda }{\frac {\lambda ^{k}}{k!}},\ k=0,1,2,\dots }
S'escriu X ∼ Poi ( λ ) {\displaystyle X\sim {\text{Poi}}(\lambda )} o X ∼ Poiss ( λ ) {\displaystyle X\sim {\text{Poiss}}(\lambda )} o alguna notació similar.

Propietats

1. Esperança i variància. L'esperança i la variància d'una variable aleatòria amb distribució de Poisson de paràmetre λ {\displaystyle \lambda } són iguals a λ {\displaystyle \lambda } :

E [ X ] = λ i Var ( X ) = λ . {\displaystyle E[X]=\lambda \quad {\text{i}}\quad {\text{Var}}(X)=\lambda .}

Així, si la distribució de Poisson s'utilitza per modelar el comptatge d'un fenomen, aleshores λ {\displaystyle \lambda } es pot interpretar com la freqüència esperada del fenomen.

Prova:

E [ X ] = ∑ k = 0 ∞ k e − λ λ k k ! = λ e − λ ∑ k = 1 ∞ λ k − 1 ( k − 1 ) ! = λ e − λ e λ = λ , {\displaystyle E[X]=\sum _{k=0}^{\infty }k\,e^{-\lambda }{\frac {\lambda ^{k}}{k!}}=\lambda \,e^{-\lambda }\sum _{k=1}^{\infty }{\frac {\lambda ^{k-1}}{(k-1)!}}=\lambda \,e^{-\lambda }e^{\lambda }=\lambda ,}
on hem utilitzat el desenvolupament es sèrie de la funció exponencial.



Per trobar el moment de segon ordre i la variància calcularem E [ X ( X − 1 ) ] {\displaystyle E[X(X-1)]} :


E [ X ( X − 1 ) ] = ∑ k = 0 ∞ k ( k − 1 ) e − λ λ k k ! = λ 2 e − λ ∑ k = 2 ∞ λ k − 2 ( k − 2 ) ! = λ 2 . {\displaystyle E[X(X-1)]=\sum _{k=0}^{\infty }k\,(k-1)\,e^{-\lambda }{\frac {\lambda ^{k}}{k!}}=\lambda ^{2}\,e^{-\lambda }\sum _{k=2}^{\infty }{\frac {\lambda ^{k-2}}{(k-2)!}}=\lambda ^{2}.}
D'altra banda,
E [ X ( X − 1 ) ] = E [ X 2 ] − E [ X ] = E [ X 2 ] − λ , {\displaystyle E[X(X-1)]=E[X^{2}]-E[X]=E[X^{2}]-\lambda ,}
d'on
E [ X 2 ] = λ 2 + λ . {\displaystyle E[X^{2}]=\lambda ^{2}+\lambda .}
Llavors,
Var ( X ) = E [ X 2 ] − ( E [ X ] ) 2 = λ . {\displaystyle {\text{Var}}(X)=E[X^{2}]-{\big (}E[X]{\big )}^{2}=\lambda .}

2. Moments d'ordre superior. Els moments d'ordre superior són polinomis de Touchard en λ {\displaystyle \lambda } , i els coeficients tenen una interpretació combinatòria. De fet, quan el valor esperat de la distribució de Poisson és 1, llavors segons la fórmula de Dobinski, el n {\displaystyle n} -èsim moment iguala el nombre de particions de mida n {\displaystyle n} .

3. Moda. La moda d'una variable aleatòria de distribució de Poisson amb un λ {\displaystyle \lambda } no sencer és igual a ⌊ λ ⌋ {\displaystyle \lfloor \lambda \rfloor } , el més gran dels enters menors que λ {\displaystyle \lambda } (els símbols ⌊     ⌋ {\displaystyle \scriptstyle \lfloor \ \ \rfloor } representen la funció part sencera). Quan λ {\displaystyle \lambda } és un enter positiu, les modes són λ {\displaystyle \lambda } i λ − 1 {\displaystyle \lambda -1} .




4. Funció generatriu de moments. La Funció generatriu de la distribució de Poisson de paràmetre λ {\displaystyle \lambda } és

E [ e t X ] = ∑ k = 0 ∞ e t k e − λ λ k k ! = e − λ ∑ k = 0 ∞ ( λ e t ) k k ! = e − λ e λ e t = e λ ( e t − 1 ) . {\displaystyle \mathrm {E} \left[e^{tX}\right]=\sum _{k=0}^{\infty }e^{tk}e^{-\lambda }{\lambda ^{k} \over k!}=e^{-\lambda }\sum _{k=0}^{\infty }{\frac {{\big (}\lambda e^{t}{\big )}^{k}}{k!}}=e^{-\lambda }\,e^{\lambda e^{t}}=e^{\lambda (e^{t}-1)}.}


Anàlogament, la funció característica és

E [ e i t X ] = e λ ( e i t − 1 ) . {\displaystyle E[e^{itX}]=e^{\lambda (e^{it}-1)}.}

5. Les variables aleatòries de Poisson són infinitament divisibles.



6. Divergència de Kullback-Leibler. La divergència Kullback-Leibler d'una variable aleatòria de Poisson de paràmetre λ 0 {\displaystyle \lambda _{0}} a una altra de paràmetre λ {\displaystyle \lambda } és

D K L ( λ | | λ 0 ) = λ ( 1 − λ 0 λ + λ 0 λ log ⁡ λ 0 λ ) . {\displaystyle D_{\mathrm {KL} }(\lambda ||\lambda _{0})=\lambda \left(1-{\frac {\lambda _{0}}{\lambda }}+{\frac {\lambda _{0}}{\lambda }}\log {\frac {\lambda _{0}}{\lambda }}\right).}

7. Sumes de variables aleatòries de Poisson. La suma de variables aleatòries de Poisson independents és una altra variable aleatòria de Poisson en què el paràmetre és la suma dels paràmetres de les originals. Dit d'una altra manera, si

X i ∼ Poi ( λ i ) , i = 1 , … , N {\displaystyle X_{i}\sim {\text{Poi}}(\lambda _{i})\,,i=1,\dots ,N}

són N variables aleatòries de Poisson independents, llavors

∑ i = 1 N X i ∼ Poi ( ∑ i = 1 N λ i ) {\displaystyle \sum _{i=1}^{N}X_{i}\sim {\text{Poi}}\left(\sum _{i=1}^{N}\lambda _{i}\right)\,}
.

Relació amb altres distribucions

Distribució binomial

La distribució de Poisson és un cas límit de la distribució binomial: una distribució binomial B ( n , p ) {\displaystyle B(n,p)} amb n {\displaystyle n} gran, p {\displaystyle p} petita, i n p {\displaystyle np} petita respecte a n {\displaystyle n} , es pot aproximar raonablement bé per una distribució de Poisson de paràmetre λ = n p {\displaystyle \lambda =np} . Històricament, Poisson va utilitzar aquest argument per introduir la seva distribució,[4] i és el principal raonament per justificar la utilització d'aquesta distribució, tal com veurem en els exemples més avall.

Formalment, sigui ( p n ) n ≥ 1 {\displaystyle (p_{n})_{n\geq 1}} una successió de nombres 0 < p n < 1 {\displaystyle 0<p_{n}<1} tals que lim n → ∞ n p n = λ > 0 {\displaystyle \lim _{n\to \infty }np_{n}=\lambda >0} . Considerem una llei binomial de paràmetres n {\displaystyle n} i p n {\displaystyle p_{n}} , X n ∼ B ( n , p n ) {\displaystyle X_{n}\sim B(n,p_{n})} , i sigui X ∼ Poi ( λ ) {\displaystyle X\sim {\text{Poi}}(\lambda )} Aleshores

lim n → ∞ P ( X n = k ) = P ( X = k ) ,   k = 0 , 1 , … {\displaystyle \lim _{n\to \infty }P(X_{n}=k)=P(X=k),\ k=0,1,\dots }


En efecte, tenim que

P ( X n = k ) = ( n k ) p n k ( 1 − p n ) n − k , k = 0 , … , n . {\displaystyle P(X_{n}=k)={n \choose k}p_{n}^{k}(1-p_{n})^{n-k},\quad k=0,\ldots ,n.}
Llavors, per a k = 0 , {\displaystyle k=0,}
lim n → ∞ P ( X n = 0 ) = lim n → ∞ ( 1 − p n ) n = lim n → ∞ ( ( 1 − p n ) 1 / p n ) n p n = e − λ = P ( X = 0 ) , {\displaystyle \lim _{n\to \infty }P(X_{n}=0)=\lim _{n\to \infty }(1-p_{n})^{n}=\lim _{n\to \infty }{\Big (}(1-p_{n})^{1/p_{n}}{\Big )}^{np_{n}}=e^{-\lambda }=P(X=0),}
on hem utilitzat un límit tipus nombre e {\displaystyle e} .

Per a qualsevol natural k ≥ 1 {\displaystyle k\geq 1} , tenim, per a n {\displaystyle n} prou gran,

P { X n = k } = n ! k ! ( n − k ) ! p n k ( 1 − p n ) n − k = n ( n − 1 ) ⋯ ( n − k + 1 ) k ! n k ( n p n ) k [ ( 1 − p n ) 1 p n ] n p n ( 1 − p n ) − k , {\displaystyle {\begin{array}{rl}P\{X_{n}=k\}&={\dfrac {n!}{k!\,(n-k)!}}p_{n}^{k}(1-p_{n})^{n-k}\\\\&={\dfrac {n(n-1)\cdots (n-k+1)}{k!\,n^{k}}}\,(np_{n})^{k}{\Big [}(1-p_{n})^{1 \over {p_{n}}}{\Big ]}^{np_{n}}(1-p_{n})^{-k},\end{array}}}
i passant al límit s'obté
P { X n = k } = λ k k ! e − λ = P ( X = k ) . {\displaystyle P\{X_{n}=k\}={\frac {\lambda ^{k}}{k!}}\,e^{-\lambda }=P(X=k).}
Noteu que d'aquí es dedueix que la successió X 1 , X 2 , … {\displaystyle X_{1},\,X_{2},\dots } convergeix en distribució a X {\displaystyle X} .


En particular, si partim de λ > 0 {\displaystyle \lambda >0} i prenem p n = λ / n {\displaystyle p_{n}=\lambda /n} aleshores tenim que una distribució binomial B ( n , p ) {\displaystyle B(n,p)} amb n {\displaystyle n} gran, n {\displaystyle n} petita i n p = λ {\displaystyle n\,p=\lambda } relativament petita respecte n {\displaystyle n} , es pot aproximar per una distribució de Poisson Poi ( λ ) {\displaystyle {\text{Poi}}(\lambda )} . Aquesta propietat fa que la distribució de Poisson també s'anomeni llei dels petits nombres; [5] o dels fenòmens rars, ja que el fenomen subjacent té probabilitat petita; Johnson and Kotz [3] atribueixen el nom <<llei del petits nombres>> a Bortkiewicz (o Borkiewitsch) (1868-1931) i el seu llibre Das Gesetz der kleinen Zahlen (La llei dels petits nombres). Un autor de pes, Feller,[6] considera desafortunat aquest nom i dona nombrosos exemples per mostrar-ho. Cal tenir present que si bé la probabilitat p {\displaystyle p} és petita, el producte n p {\displaystyle n\,p} pot ser gran, sempre que sigui relativament petit respecte de n {\displaystyle n} .

Aproximació normal

A conseqüència de teorema central del límit, per a valors grans de λ {\displaystyle \lambda } , una variable aleatòria de Poisson X {\displaystyle X} es pot aproximar per una variable normal de mitjana i variància λ {\displaystyle \lambda } ja que

lim λ → ∞ X − λ λ = N ( 0 , 1 ) ,   en distribució . {\displaystyle \lim _{\lambda \to \infty }{\frac {X-\lambda }{\sqrt {\lambda }}}=N(0,1),\ {\text{en distribució}}.}
Vegeu .[7][8]

Distribució exponencial

Suposem que per a cada valor t > 0 {\displaystyle t>0} , que representa el temps, el nombre d'aparicions de cert fenomen aleatori segueix una distribució de Poisson de paràmetre λ t {\displaystyle \lambda t} . Llavors, els temps que discorren entre dos aparicions successives segueix la distribució exponencial.

Distribució khi-quadrat χ 2 {\displaystyle {\boldsymbol {\chi }}^{2}}

Si X {\displaystyle X} és una distribució de Poisson de paràmetre λ {\displaystyle \lambda } , aleshores [9] per a k = 0 , 1 , 2 , … {\displaystyle k=0,\,1,2,\dots } ,

P ( X ≤ k ) = P ( χ 2 ( k + 1 ) 2 > 2 λ ) , {\displaystyle P(X\leq k)=P(\chi _{2(k+1)}^{2}>2\lambda ),}

on χ 2 ( k + 1 ) 2 {\displaystyle \chi _{2(k+1)}^{2}} és una variable aleatòria amb distribució χ 2 {\displaystyle \chi ^{2}} amb 2 ( k + 1 ) {\displaystyle 2(k+1)} graus de llibertat.

Aquesta fórmula és útil perquè permet calcular el valor de la funció de distribució d'una variable aleatòria de Poisson de manera ràpida.

Exemples històrics

Soldats de l'exèrcit prussià morts per una guitza del seu cavall

En el llibre que hem citat abans de Bortkiewicz, s'estudia el nombre de soldats de l'exèrcit prussià morts per una guitza del seu cavall. A la taula[10] hi ha el nombre de morts corresponent a 10 cossos de característiques similars [11] durant 20 anys


Taula 1. Nombre de soldats morts per una guitza del seu cavall a l'exercit en 10 cossos de l'exercit prussià durant 1875-1894
Cos de l'exercit
Any II III IV V VII VIII IX X XIV XV Total
1875 1 1 1 3
1876 1 1 1 3
1877 1 1 2 4
1878 2 1 1 1 1 6
1879 1 1 2 1 1 6
1880 2 1 1 1 2 1 3 11
1881 2 1 1 1 5
1882 1 1 2 4 1 9
1883 1 2 1 1 1 6
1884 1 1 2 1 1 6
1885 2 1 3
1886 1 1 1 3 6
1887 2 1 2 1 1 2 9
1888 1 1 1 3
1889 1 1 1 1 2 2 8
1890 2 1 2 2 1 2 2 12
1891 1 1 1 1 1 3 1 9
1892 2 1 1 1 1 1 7
1893 1 2 1 4
1894 1 1 2
Total 12 12 8 11 12 7 13 15 24 8 122

En total es van produir 122 morts. La següent taula és un resum de la Taula 1 en termes de freqüències absolutes i relatives:

Taula 2. Taula de freqüències de les dades de Bortkiewicz
Nombre de soldats morts en un cos i anys 0 1 2 3 4 Total
Freqüència absoluta 109 65 22 3 1 200
Freqüència relativa 0.545 0,325 0,110 0,015 0,005 1

La mitjana de morts per cos i any és

X ¯ = 0 ⋅ 109 + 1 ⋅ 65 + 2 ⋅ 22 + 3 ⋅ 3 + 4 ⋅ 1 200 = 122 200 = 0 , 61. {\displaystyle {\overline {X}}={\frac {0\cdot 109+1\cdot 65+2\cdot 22+3\cdot 3+4\cdot 1}{200}}={\frac {122}{200}}=0,61.}

Suposem que cos de l'exèrcit tenia 1000 soldats (com veurem, aquest nombre, que desconeixem, no té cap paper, podríem posar n {\displaystyle n} ). Un model raonable per al nombre de soldats morts (per cos i any) és una distribució binomial B ( 1000 , p ) {\displaystyle B(1000,p)} , on p {\displaystyle p} és la probabilitat que un soldat resulti mort. Aquesta probabilitat és molt petita i podem estimar-la de la següent manera: Tenim 10 cossos durant 10 anys, que representen 10 × 20 × 1000 = 200.000 {\displaystyle 10\times 20\times 1000=200.000} soldats. Aleshores

p = nombre de soldats morts nombre total de soldats = 122 200000 = 0 , 00061. {\displaystyle p={\frac {\text{nombre de soldats morts}}{\text{nombre total de soldats}}}={\frac {122}{200000}}=0,00061.}
D'acord amb els comentaris anteriors, podem aproximar la distribució binomial per una distribució de Poisson de paràmetre
λ = n × p = 1000 × 0 , 00061 = 0 , 61 , {\displaystyle \lambda =n\times p=1000\times 0,00061=0,61,}
que és la mitjana que hem calculat abans. La Taula 3 dona les probabilitats d'una variable aleatòria de Poisson X {\displaystyle X} de paràmetre λ = 0 , 61 {\displaystyle \lambda =0,61} , X ∼ Poi ( 0 , 61 ) {\displaystyle X\sim {\text{Poi}}(0,61)} :

Taula 3. Taula de probabilitats d'una distribució de Poisson Poi(0,61)
X {\displaystyle X} 0 1 2 3 ≥ 4 {\displaystyle \geq 4}
Probabilitat 0.543 0,331 0,101 0,020 0,003

En comparar la fila de les freqüències relatives de la Taula 2 i les probabilitats de la Taula 3 veiem que la concordança entre ambdues és realment notable.

Desintegració de partícules radioactives

Rutherford i Geiger [12] reporten que varen observar el nombre de partícules α {\displaystyle \alpha } emeses per una massa de material radioactiu durant 2.608 intervals de 7,5 segons cadascun. A la Taula 4 la k {\displaystyle k} denota el nombre de partícules emeses en un interval de 7,5 segons, la freqüència absoluta és el nombre de vegades que es va observar el corresponent valor k {\displaystyle k} , després hi ha freqüència relativa i finalment la probabilitat que una variable de Poisson de paràmetre λ = 3 , 87 {\displaystyle \lambda =3,87} prengui aquell valor:

Taula 4. Experiment de Rutherford et al.
k {\displaystyle k} 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 Total
Freq. absoluta 57 203 383 525 532 408 273 139 45 27 10 4 0 1 1 2608
Freq. relativa 0,022 0,078 0,147 0,201 0,204 0,156 0,105 0,053 0,017 0,010 0.004 0.002 0.000 0,000 0,000 1
Probabilitat Poisson 0,021 0,081 0,156 0,201 0,195 0,151 0,097 0,054 0,026 0,011 0.004 0.002 0.000 0,000 0,000 1



El paràmetre λ {\displaystyle \lambda } s'ha calculat com la mitjana del nombre de partícules emeses per unitat de temps:

λ = X ¯ = 0 × 57 + 1 × 203 + ⋯ 2608 = 10097 2608 = 3 , 87. {\displaystyle \lambda ={\overline {X}}={\frac {0\times 57+1\times 203+\cdots }{2608}}={\frac {10097}{2608}}=3,87.}

Com veiem la concordança entre les dades observades i les probabilitats corresponents a la distribució de Poisson és molt bona. Breiman [13] argumenta perquè la distribució de Poisson apareix en aquesta situació: Suposem que durant un període llarg, la mitjana de partícules emeses per unitat de temps és λ {\displaystyle \lambda } (en aquest cas, la unitat de temps seria 7,5 seg). Considerem ara el nombre de partícules emeses durant un interval de temps de longitud t {\displaystyle t} unitats; el resultat pot ser 0, 1, 2, etc. Per trobar una assignació raonable de probabilitats dividim l'interval [ 0 , t ] {\displaystyle [0,t]} en n {\displaystyle n} parts d'amplada t / n {\displaystyle t/n} ; prenem n {\displaystyle n} prou gran perquè els subintervals siguin molt petits; en cada subinterval podem observar 0, 1, 2, ... partícules. Suposem:



1. Les probabilitats d'observar 0, 1, ... partícules són les mateixes per a tots els subintervals.

2. La probabilitat d'observar dos o més partícules en un subinterval és menyspreable comparada amb les probabilitats d'observar-ne zero o una partícula.

3. La probabilitat d'observar o no una partícula en un subinterval és independent d'observar o no una partícula en un altre subinterval.

El bombardeig de Londres durant la 2a. Guerra Mundial

Durant la Segona Guerra Mundial els alemanys van bombardejar Londres i altres llocs amb bombes volants. Molta gent creia que les bombes tendien a agrupar-se en clústers; amb l'objectiu d'analitzar si aquesta suposició era veritat es va dividir el sud de Londres en 576 quadrats de 0'5 km²; durant el període considerat van caure 537 bombes, vegeu la Figura 1.

Figura 1. Part de la quadrícula del mapa de Londres amb els impactes de les bombes volants (punts simulats per ordinador). En total hi havia 576 quadrats, cadascun de 0'5 km²

La taula 5 [14] mostra el nombre de quadrats on van caure 0 bombes, 1 bomba, etc. (freqüència absoluta), així com la freqüència relativa.



Taula 5. Bombardeig sobre Londres
k {\displaystyle k} 0 1 2 3 4 ≥ 5 {\displaystyle \geq 5} Total
Freq. absoluta 229 211 93 35 7 1 576
Freq. relativa 0,397 0,366 0,161 0,061 0,012 0,002 1
Prob. Poisson 0,394 0,367 0,171 0,053 0,012 0,002 1
Freq. esperada Poisson 226,7 211,4 98,5 36,6 7,1 1,3 575,8

La mitjana de bombes per quadrat és

X ¯ = 537 576 ≈ 0 , 932. {\displaystyle {\overline {X}}={\frac {537}{576}}\approx 0,932.}
A la taula 5 hi ha una fila amb les probabilitats P ( X = k ) {\displaystyle P(X=k)} d'una variable de Poisson X {\displaystyle X} de paràmetre λ = 0 , 932 {\displaystyle \lambda =0,932} per k = 0 , 1 , … , 4 {\displaystyle k=0,1,\dots ,4} i el valor P ( X ≥ 5 ) {\displaystyle P(X\geq 5)} . També hi ha una fila amb els productes
576 × P ( X = k ) , k = 0 , 1 , … , 4 i 576 × P ( X ≥ 5 ) , {\displaystyle 576\times P(X=k),\quad k=0,1,\dots ,4\quad {\text{i}}\quad 576\times P(X\geq 5),}
els quals són les freqüències absolutes esperades per una variable de Poisson.

L'ajustament de les dades observades amb les donades per la distribució de Poisson és molt bona, la qual cosa suggereix que no va haver-hi clústers i que el lloc de caiguda de les bombes era completament aleatori. Chung[15] argumenta el bon ajust amb la distribució de Poisson dient que, si el fenomen és purament aleatori, es pot estudiar com un problema de col·locació de 537 objectes en 576 caixes; la probabilitat d'observar exactament k {\displaystyle k} bombes (objectes) en un quadrat (una capsa) serà P ( Y = k ) {\displaystyle P(Y=k)} , on Y {\displaystyle Y} és una variable binomial de paràmetres n = 537 {\displaystyle n=537} i p = 1 / 576 {\displaystyle p=1/576}  : Y ∼ B ( 537 , 1 / 576 ) {\displaystyle Y\sim B(537,1/576)} . Atès que n {\displaystyle n} és gran i p {\displaystyle p} petita, podem aproximar Y {\displaystyle Y} per una variable de Poisson de paràmetre

λ = n p = 537 × 1 576 ≈ 0 , 932 , {\displaystyle \lambda =n\,p=537\times {\frac {1}{576}}\approx 0,932,}
que és el que hem fet anteriorment.

Feller [16] també analitza aquestes dades i comenta que <<la taula anterior indica que hi ha aleatorietat i homogeneïtat perfectes, [...] però que per a [l'ull] inexpert, l'aleatorietat apareix com regularitat [...]>>. Per profunditzar en aquest comentari de Feller és molt interessant el capítol 2 del llibre de J. A. Paulos [17]

Més exemples

Si el 2% dels llibres enquadernats en cert taller té enquadernació defectuosa, la probabilitat que 5 de 400 llibres enquadernats en aquest taller tinguin enquadernacions defectuoses es pot calcular usant la distribució de Poisson. En efecte, el nombre de llibres defectuosos es pot modelar per una distribució binomial de paràmetres n = 400 {\displaystyle n=400} i p = 0 , 02 {\displaystyle p=0,02} , la qual el pot aproximar per una distribució de Poisson de paràmetre

λ = 400 × 0.02 = 8 , {\displaystyle \lambda =400\times 0.02=8,}
que, d'altra banda, és la mitjana de llibres defectuosos. Per tant, la probabilitat desitjada és

P ( X = 5 ) = 8 5 e − 8 5 ! = 0 , 092. {\displaystyle P(X=5)={\frac {8^{5}e^{-8}}{5!}}=0,092.}

Aquest problema també podria resoldre's recorrent a una distribució binomial de paràmetres k = 5 {\displaystyle k=5} , n = 400 {\displaystyle n=400} i p = 0 , 02 {\displaystyle p=0,02} .

Processos de Poisson

La distribució de Poisson s'aplica a diversos fenòmens discrets de la natura (és a dir, aquells fenòmens que ocorren 0, 1, 2, 3, ... vegades durant un període definit de temps o en una àrea determinada) quan la probabilitat d'ocurrència del fenomen és constant en el temps o l'espai. Exemples d'aquests esdeveniments que poden ser modelats per la distribució de Poisson inclouen:

  • El nombre de cotxes que passen a través d'un cert punt en una ruta (prou distants dels semàfors) durant un període definit de temps.
  • El nombre d'errors d'ortografia que un comet en escriure una única pàgina.
  • El nombre de trucades telefòniques en una central telefònica per minut.
  • El nombre de servidors web accedits per minut.
  • El nombre d'animals morts trobats per unitat de longitud de ruta.
  • El nombre de mutacions de determinada cadena d'ADN després de certa quantitat de radiació.
  • El nombre de nuclis atòmics inestables que van decaure en un determinat període en una porció de substància radioactiva. La radioactivitat de la substància es debilitarà amb el temps, per tant el temps total de l'interval utilitzat en el model ha de ser significativament menor que la vida mitjana de la substància.
  • El nombre d'estels en un determinat volum d'espai.
  • El nombre d'estels fugaços per una unitat de temps.
  • La distribució de receptors visuals a la retina de l'ull humà.
  • La inventiva d'un inventor a través de la seva carrera.[18]

Vegeu també

Referències

  1. ↑ Poisson, Siméon-Denis (1781-1840) Auteur du texte. Recherches sur la probabilité des jugements en matière criminelle et en matière civile ; précédées des Règles générales du calcul des probabilités / par S.-D. Poisson,... (en francès), 1837. 
  2. ↑ Feller, W.. Introducción a la teoría de las probabilidades y sus aplicaciones. México: Limusa-Wiley, S. A.. 
  3. ↑ 3,0 3,1 Johnson, Norman Lloyd. Univariate discrete distributions.. 2nd ed.. Nova York: Wiley, 1992. ISBN 0-471-54897-9. 
  4. ↑ Poisson, Siméon-Denis (1781-1840) Auteur du texte. Recherches sur la probabilité des jugements en matière criminelle et en matière civile ; précédées des Règles générales du calcul des probabilités / par S.-D. Poisson,... (en francès), 1837, p. 205. 
  5. ↑ L. von Bortkiewicz, <<Das Gesetz der Klenen Zahlen>> (1898), citat per Jonhson, N. L. and Kotz, S. <<Univariate Discrete Distributions>>, 2nd edition, Wiley (1992)
  6. ↑ Feller, W.. Introducción a la teoría de las probabilidades y sus aplicaciones. México: Limusa-Wiley, S. A., p. 169. 
  7. ↑ Feller, W.. Introducción a la Teoría de las Probabilidades y sus aplicaciones. México: Limusa-Wiley, S. A., 1973, p. 253. 
  8. ↑ Hoffmann-Jørgensen, J. Probability with a view toward statistics. New York, NY: Chapman & Hall, ©1994-, p. 412. ISBN 0-412-05221-0. 
  9. ↑ Johnson, Norman Lloyd. Univariate discrete distributions.. 2nd ed.. Nova York: Wiley, 1992, p. 162, formula (4.38). ISBN 0-471-54897-9. 
  10. ↑ Andrews, D. F.. Data : a Collection of Problems from Many Fields for the Student and Research Worker. New York, NY: Springer New York, 1985, p. 18. ISBN 978-1-4612-5098-2. 
  11. ↑ De la taula original s'han exclòs les columnes corresponents als cossos G, I, VI i XI perquè tenien característiques diferents
  12. ↑ F.R.S, Professor E. Rutherford; Ph.D, H. Geiger; Bateman, H. «LXXVI. The probability variations in the distribution of α particles». The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 20, 118, 01-10-1910, pàg. 698–707. DOI: 10.1080/14786441008636955. ISSN: 1941-5982.
  13. ↑ Breiman, Leo. Statistics: with a view toward applications.. Boston,: Houghton Mifflin, 1973. ISBN 0-395-04232-1. 
  14. ↑ CLARKE, R. D. «AN APPLICATION OF THE POISSON DISTRIBUTION». Journal of the Institute of Actuaries (1886-1994), 72, 3, 1946, pàg. 481–481. ISSN: 0020-2681.
  15. ↑ Lai Chung, Kai. Teoría elemental de la probabilidad y de los procesos estocásticos. Barcelona: Reverté, 1983, p. 231-233. ISBN 84-291-5049-8. 
  16. ↑ Feller, W.. Introducción a la Teoría de las Probabilidades y sus aplicaciones. México: Limusa- Wiley, S. A., 1973, p. 170-171. 
  17. ↑ Paulos, John Allen. El hombre anúmerico : el analfabetismo matemático y sus consecuencias. 4a. ed. Barcelona: Tusquets, 1998. ISBN 84-7223-149-6. 
  18. ↑ [enllaç sense format] http://www.leaonline.com/doi/pdfplus/10.1207/s15326934crj1103_3
  • Vegeu aquesta plantilla
Distribucions discretes
amb suport finit
Distribucions discretes
amb suport infinit
Distribucions contínues
suportades sobre un interval acotat
Distribucions contínues
suportades sobre un interval semi-infinit
Distribucions contínues
suportades en tota la recta real
Distribucions contínues
amb el suport de varis tipus
Barreja de distribució variable-contínua
Distribució conjunta
Discreta
Ewens
Multinomial
Multinomial de Dirichlet
Multinomial negativa
Contínua
Dirichlet
Dirichlet generalitzada
Estable multivariant
Gamma normal
Gamma normal inversa
Normal multivariable
t multivariable
Matriu de valor
Matriu gamma
Matriu gamma inversa
Matriu normal
Normal de Wishart
Normal de Wishart inversa
t matriu
Wishart
Wishart inversa
Direccionals
Univariada (circular)
Asimètrica de Laplace envoltada
Cauchy envoltada
Exponencial envoltada
Lévy envoltada
Normal envoltada
Circular uniforme
Univariada de von Mises
Bivariada (esfèrica)
Kent
Bivariada (toroidal)
Bivariada de von Mises
Multivariada
von Mises-Fisher
Bingham
Degenerada i singular
Degenerada
Delta de Dirac
Singular
Cantor
Famílies