Korda

Korda (från latin chorda, "sträng")^[2] är den räta linje som sammanbinder två punkter på en cirkelbåge eller annan kroklinje.^[3] Historiskt användes också korda som en trigonometrisk funktion, nämligen längden av den korda som i en cirkel med fix radie motsvarar en medelpunktsvinkel. Uttryckt i moderna termer är denna korda av vinkeln v detsamma som 2r sin (v/2), där r är cirkelns radie.

En korda delar cirkelns yta i två cirkelsegment. En korda genom cirkelns medelpunkt, som är den längsta möjliga kordan, kallas diameter.

Kordasatsen

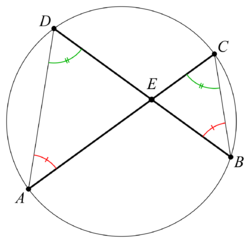
Med hjälp av bland annat teorin för likformiga trianglar kunde man i den hellenistiska antika matematiken bevisa olika samband som involverar kordor. Bland dessa finns kordasatsen, enligt vilken om två kordor i samma cirkel skär varandra, så är produkten av längderna av de två segmentdelarna i den ena kordan lika stor som motsvarande produkt i den andra:

${\displaystyle |{\overline {EB}}|\cdot |{\overline {ED}}|=|{\overline {EA}}|\cdot |{\overline {EC}}|}$

eftersom trianglarna ${\displaystyle \textstyle \triangle ADE}$ och ${\displaystyle \textstyle \triangle BCE}$ är likformiga, ty:

${\displaystyle \angle AED=\angle BEC}$ eftersom de är motstående vinklar i ${\displaystyle E}$

${\displaystyle \angle ADB=\angle ACB}$ eftersom de båda spänner över kordan ${\displaystyle {\overline {AB}}}$ på samma sida (se randvinkelsatsen)

${\displaystyle \angle CAD=\angle CBD}$ eftersom de båda spänner över kordan ${\displaystyle {\overline {CD}}}$ på samma sida

Kordan som trigonometrisk funktion

Kordafunktionen ${\displaystyle {\mbox{crd}}}$ anger kordans längd i en enhetscirkel för en given medelpunktsvinkel. Den kan spåras redan på kilskriftstavlor från Mesopotamien. Under 100-talet gjorde astronomen och matematikern Klaudios Ptolemaios från Alexandria upp en noggrann kordatabell, som ingick i hans huvudverk Almagest.^[4] Ptolemaios anger kordorna för alla halva och hela vinklar upp till ett halvt varv i en cirkel med radien 60 längdenheter. Sambandet med de moderna trigonometriska funktionerna är:

${\displaystyle {\mbox{crd}}\ \theta =2\sin {\frac {\theta }{2}}}$ eftersom bisektrisen till ${\displaystyle \theta }$ är mittpunktsnormal till kordan.

Ett specialfall är en rätvinklig triangel då

${\displaystyle \theta ={\frac {\pi }{2}}\Rightarrow {\mbox{crd}}\ \theta ={\sqrt {2}}}$.

Den inversa funktionen existerar också:

${\displaystyle \operatorname {acrd} (y)=2\arcsin \left({\frac {y}{2}}\right)\,}$^[5]

Identiteter

Kordafunktionen har många identiteter som är analoga med sinusfunktionen:

Identitet	Uttryckt med sinus	Uttryckt med korda
Trigonometriska ettan	${\displaystyle \sin ^{2}\theta +\cos ^{2}\theta =1}$	${\displaystyle {\mbox{crd}}^{2}\theta +{\mbox{crd}}^{2}(180^{\circ }-\theta )=4}$
Halva vinkeln	${\displaystyle \sin {\frac {\theta }{2}}=\pm {\sqrt {\frac {1-\cos \theta }{2}}}}$	${\displaystyle {\mbox{crd}}\ {\frac {\theta }{2}}=\pm {\sqrt {2-{\mbox{crd}}(180^{\circ }-\theta )}}}$

Kordor och kägelsnitt

Mittpunkterna på alla med varandra parallella kordor i en cirkel, ellips eller annat kägelsnitt är kollinjära, vilket visades av Apollonios under tredje århundradet f.Kr. i första boken av Κωνικά, Konika.^[6] Denna sammanbindningslinje kallade Apollonios diameter (διαμέτρος, diametros - "diameter" är en latinisering)^[7], ett begrepp som fortfarande används.

Beviset för en cirkel görs enklast geometriskt, eftersom alla kordor som är parallella har samma diameter som mittpunktsnormal; vilket i stort sett är hela beviset.

Beviset för en ellips följer direkt ur beviset för cirkeln: utgå från en cirkel med samma radie som halva lillaxeln, "töj" sedan ut cirkeln i "storaxel-ledd" (eller ändra längdskalan i denna ledd!) till den önskade ellipsen - kordor som var parallella i cirkeln är fortfarande parallella i ellipsen och låg kordonas mittpunkter på en linje i cirkeln, vilket de gjorde, kommer de att ligga på en linje även i ellipsen. Töjning (skalning i en riktning) är en affin avbildning och kollinearitet, parallellitet och relativa avstånd mellan punkter på en linje tillhör de egenskaper som bevaras under en sådan.

Nedan ges ett bevis för parabler, att det gäller även för hyperbler kan visas analogt (enklast visat för hyperbeln ${\displaystyle \textstyle y={\frac {1}{x}}}$ eftersom alla andra hyperbler är affina avbildningar av denna).

Bevis för en parabel

Givet en parabel. Välj ett kartesiskt koordinatsystem sådant att origo ${\displaystyle (0,0)}$ ligger i parabelns spets och punkten ${\displaystyle (0,1)}$ i dess fokus. Vi har då parabelns ekvation:

${\displaystyle y={\frac {x^{2}}{4}}}$

En korda är en rät linje, så låt kordan (som inte ju kan vara vertikal, eftersom den då inte skär parabeln i två punkter) ha ekvationen

${\displaystyle y=ax+b}$

Alla parallella kordor har samma riktningskoeffecient ${\displaystyle a}$ och endast värdet på ${\displaystyle b}$ (var de skär y-axeln) skiljer dem sålunda.

Lösning av

${\displaystyle y={\frac {x^{2}}{4}}=ax+b\Leftrightarrow x^{2}-4ax-4b=0}$

ger de båda skärningspunkterna mellan parabeln och kordan

${\displaystyle x_{1}={\sqrt {4a^{2}+4b}}+2a}$

${\displaystyle x_{2}=-{\sqrt {4a^{2}+4b}}+2a}$

Låt ${\displaystyle (x_{m},y_{m})}$ beteckna mittpunkten på kordan, då är

${\displaystyle x_{m}={\frac {x_{1}+x_{2}}{2}}=2a}$

De olika kordornas mittpunkter har alltså samma x-värde eftersom de har samma riktningskoefficient, vilket innebär att alla ligger på den vertikala räta linjen genom ${\displaystyle (2a,0)}$.

Vi har också att

${\displaystyle {\begin{aligned}y_{m}&={\frac {y_{1}+y_{2}}{2}}={\frac {x_{1}^{2}}{2\cdot 4}}+{\frac {x_{2}^{2}}{2\cdot 4}}=\\&={\frac {({\sqrt {4a^{2}+4b}}+2a)^{2}+(-{\sqrt {4a^{2}+4b}}+2a)^{2}}{8}}=\\&={\frac {2(4a^{2}+4b)+2(4a^{2})}{8}}=\\&=2a^{2}+b\end{aligned}}}$

Viket visar att avståndet mellan kordorna i y-ledd är skillnaden i värdet på ${\displaystyle b}$, något vi redan visste, och att mittpunkten för en korda med ekvationen ${\displaystyle y=ax+b}$ ligger i punkten ${\displaystyle (2a,\ 2a^{2}+b)}$.

Se även

Wiktionary har en ordboksartikel om korda.

• Periferi
• Rand (geometri)
• Sinus

Referenser

Noter