Konvex mängd

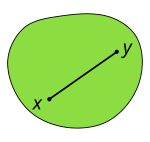
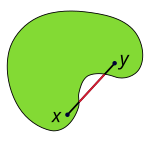
En mängd i ett reellt eller komplext vektorrum är konvex om varje punkt längs en sträcka mellan två godtyckligt valda punkter i mängden också ligger i mängden. Man kan även uttrycka det som att alla andra punkter går att "se" från varje punkt i mängden.

Konvex mängd är ett begrepp som är vanligt förekommande inom optimeringsläran och olika grenar av mängdläran.

Definition

En mängd X i ett reellt eller komplext vektorrum sägs vara konvex om

${\displaystyle x_{1},x_{2}\in X\quad }$

implicerar att

${\displaystyle \lambda x_{1}+(1-\lambda )x_{2}\in X\quad \forall \quad \lambda \in [0,1]}$

Med andra ord ska linjestycket mellan ${\displaystyle x_{1}}$ och ${\displaystyle x_{2}}$ ligga i X. ^[1][2][3]

Egenskaper

Konvexkombinationer

Om ${\displaystyle x_{1},x_{2},...,x_{n}}$ är punkter i ett reellt eller komplext vektorrum är en konvexkombination av dessa punkter en punkt som kan skrivas som:

${\displaystyle \sum _{i=1}^{n}\lambda _{i}x_{i}\quad \forall \lambda _{i}>0;\ i=1,2,...,n\quad \mathrm {med} \quad \sum _{i=1}^{n}\lambda _{i}=1}$

En mängd är konvex om och endast om den innehåller alla sina konvexkombinationer. ^[4]

Skärning mellan konvexa mängder

Snittet mellan ett ändligt antal konvexa mängder är också konvext.

Bevis

Låt ${\displaystyle C_{1},C_{2},...,C_{k}}$ vara en samling konvexa mängder och låt mängden D definieras enligt nedan:

${\displaystyle D=\bigcap _{i=1}^{k}\ C_{i}}$

Då önskar man visa att för två godtyckliga punkter x₁ och x₂ i D så gäller att

${\displaystyle \lambda x_{1}+(1-\lambda )x_{2},\ \lambda \in [0,1]}$

också ligger i D.

Man vet att om ${\displaystyle x_{1},x_{2}}$ är två element i D så är ${\displaystyle x_{1},x_{2}}$ också två element i alla de konvexa mängderna ${\displaystyle C_{1},C_{2},...,C_{k}}$.

Således, eftersom ${\displaystyle C_{1},C_{2},...,C_{k}}$ är konvexa, så ligger

${\displaystyle \lambda x_{1}+(1-\lambda )x_{2},\ \lambda \in [0,1]}$

i varje en av mängderna ${\displaystyle C_{1},C_{2},...,C_{k}}$.

Därför vet man att

${\displaystyle \lambda x_{1}+(1-\lambda )x_{2},\ \lambda \in [0,1]}$

ligger inom skärningen mellan ${\displaystyle C_{1},C_{2},...,C_{k}}$, dvs inom mängden D som då också är konvex. ^[5]

Konvext hölje

För varje mängd X i ett reellt eller komplext vektorrum finns en minsta konvex mängd som innehåller mängden. Denna mängd kallas för X:s konvexa hölje. Det konvexa höljet till X kan ses som snittet av alla konvexa mängder som innehåller X, eller som mängden av alla konvexkombinationer av punkterna i X. ^[6]

Stjärnformighet

Om C är ett godtyckligt reellt eller komplext vektorrum i ett ändligt antal dimensioner gäller det att C är stjärnkonvex om det finns något ${\displaystyle x_{0}}$ i C sådant att konvexkombinationen av ${\displaystyle x_{0}}$ och alla andra punkter i C ligger inom C.

Således vet man att en konvex mängd alltid är stjärnformig, men stjärnformiga mängder är inte alltid konvexa.

Tillämpningar

Konvexa mängder, tillsammans med konvexa funktioner används för att lösa flera typer av problem inom flera olika matematiska områden.

Simplexmetoden

Simplexmetoden används för att lösa LP-problem vars allmänna form är:

${\displaystyle \min \ z=\sum _{j=1}^{n}c_{j}x_{j}}$

med bivillkor enligt:

${\displaystyle \sum _{j=1}^{n}a_{ij}x_{j}\leq b_{i}\ ,\quad 1=1,...,m}$

${\displaystyle x_{j}\geq 0\ ,\quad j=1,...,n}$

Ovan så är ${\displaystyle c_{j}}$ koefficienten i målfunktionen för variabeln ${\displaystyle x_{j}}$. ${\displaystyle a_{i}j}$ är motsvarande koefficient i bivillkor i, och ${\displaystyle b_{i}}$ är motsvarande högerledskoefficient.

Sats

Det tillåtna området (området som definieras av bivillkoren) i ett LP-problem utgör en konvex mängd.

Bevis

Låt ${\displaystyle x^{(1)},x^{(2)}}$ vara två godtyckliga punkter som är tillåtna under samtliga bivillkor i. Detta kan skrivas som att

${\displaystyle \sum _{j=1}^{n}a_{ij}x_{j}^{(1)}\leq b_{i}\quad {\mbox{och}}\quad \sum _{j=1}^{n}a_{ij}x_{j}^{(2)}\leq b_{i}}$

Betrakta sedan en punkt på linjen mellan ${\displaystyle x^{(1)},x^{(2)}}$ som är en konvexkombination av de båda punkterna, dvs en punkt

${\displaystyle x=(1-\lambda )x^{(1)}+\lambda x^{(2)},{\mbox{ med }}\lambda \in [0,1]}$

Multiplicera sedan de båda olikheterna ovan med ${\displaystyle (1-\lambda )}$ respektive ${\displaystyle \lambda }$ och addera de båda. Detta ger:

${\displaystyle (1-\lambda )\sum _{j=1}^{n}a_{ij}x_{j}^{(1)}+\lambda \sum _{j=1}^{n}a_{ij}x_{j}^{(2)}\leq (1-\lambda )b_{i}+\lambda b_{i}=b_{i}}$

och detta kan skrivas:

${\displaystyle \sum _{j=1}^{n}a_{ij}[(1-\lambda )x_{j}^{(1)}+\lambda x_{j}^{(2)}]\leq b_{i}}$

Detta säger att även den godtyckliga punkten är tillåten med avseende på bivillkor i, och detta är definitionen på en konvex mängd. En slutsats som kan dras av detta är att mängden av alla lösningar till villkoret

${\displaystyle \sum _{j=1}^{n}a_{ij}x_{j}\leq b_{i}}$

då utgör en konvex mängd. Detta resonemang kan tillämpas på alla övriga bivillkor till det allmänna LP-problemet, vilket ger slutsatsen att det tillåtna området i ett LP-problem är en konvex mängd. ^[7]

Se även

• Konvex funktion

Källor

Externa länkar

• Wikimedia Commons har media som rör Konvex mängd.
  Bilder & media