Tensor de curvatura de Riemann

Em geometria diferencial, tensor de curvatura é uma das noções métricas mais importantes. Um tensor de curvatura é uma generalização da curvatura de Gauss em dimensões mais altas (dois exemplos disto são o tensor de Riemann que se desenvolve neste artigo e o tensor de Ricci).

A geometria infinitesimal das variedades de Riemann com dimensão ≥ 3 é demasiado complicada para ser descrita totalmente por um número em um ponto dado (tal como sucede quando a dimensão é menor ou igual a 2). Assim em 2 dimensões a curvatura pode ser representada por um número escalar (ou tensor de ordem zero), em 3 dimensões a curvatura pode ser representada por um tensor de segunda ordem (como por exemplo o tensor de Ricci). Entretanto para dimensões totalmente gerais se necessita ao menos um tensor de quarta ordem (como o tensor de Riemann). Foi Riemann quem introduziu uma maneira de descrever completamente a curvatura em qualquer número de dimensões mediante um "pequeno monstro" de tensor, chamado tensor de Riemann.

Descrição

Definição geral

Seja ${\displaystyle M}$ uma variedade diferenciável dotada de uma conexão ${\displaystyle \nabla }$, definida em um ponto ${\displaystyle p}$ da variedade. O tensor de Riemann é o campo tensorial ${\displaystyle R}$ de tipo (1,3) que satisfaz a igualdade

em que ${\displaystyle X,Y,Z}$ são campos vetoriais em ${\displaystyle M_{p}}$, sendo ${\displaystyle [X,Y]}$ o colchete de Lie dos campos vetoriais. ${\displaystyle R(X,Y)Z}$ é linear em ${\displaystyle X,Y,Z}$, de modo que o valor de ${\displaystyle R(X,Y)Z}$ em ${\displaystyle p}$ só depende dos valores de ${\displaystyle X,Y}$ e ${\displaystyle Z}$ em ${\displaystyle p}$.^[1] É importante destacar que o tensor de Riemann é algumas vezes representado pelo sinal oposto.

O teorema de Schwarz afirma que no espaço euclidiano as derivadas parciais comutam: este fato não é verdade em uma variedade com conexão arbitrária, e o tensor de Riemann leva isso em consideração. Então, é possível interpretar o tensor de curvatura de Riemann como o modo de medir o quanto a variedade ${\displaystyle M}$ difere de um espaço euclidiano, ou de um espaço de Minkowski no contexto da relatividade. Logo, um espaço é dito plano quando o tensor de Riemann é zero.

Considerando um sistema de coordenadas ${\displaystyle \{x^{i}\}}$, em que ${\displaystyle X=\partial /\partial x^{i}}$ e ${\displaystyle Y=\partial /\partial x^{j}}$. Então, ${\displaystyle [X,Y]=0}$ e portanto a fórmula simplifica como

${\displaystyle R(X,Y)Z=\nabla _{X}\nabla _{X}Z-\nabla _{Y}\nabla _{X}Z}$,

ou seja, neste caso o tensor de curvatura mede a não-comutatividade da derivada covariante.^[2]

Expressão em coordenadas

Considerando a base coordenada ${\displaystyle \{\mathbf {e} _{\mu }\}}$ e sua correspondente dual ${\displaystyle \{\mathrm {d} x^{\kappa }\}}$, o tensor de Riemann pode ser expresso como

${\displaystyle {R^{\kappa }}_{\lambda \mu \nu }=\left\langle \mathrm {d} x^{\kappa },R\left(\mathbf {e} _{\mu },\mathbf {e} _{v}\right)\mathbf {e} _{\lambda }\right\rangle =\left\langle \mathrm {d} x^{\kappa },\nabla _{\mu }\nabla _{\nu }\mathbf {e} _{\lambda }-\nabla _{\nu }\nabla _{\mu }\mathbf {e} _{\lambda }\right\rangle }$,

em que ${\displaystyle \langle .,.\rangle }$ representa o produto interno.

Deste modo, a expressão pode ser representada em termos de coordenadas usando os símbolos de Christoffel. Valendo-se da convenção do somatório de Einstein, pode-se representá-lo como

${\displaystyle {R^{\kappa }}_{\lambda \mu \nu }={\partial _{\mu }{\Gamma ^{\kappa }}_{\nu \lambda }}-{\partial _{\nu }{\Gamma ^{\kappa }}_{\mu \lambda }}+{\Gamma ^{\eta }}_{\nu \lambda }{\Gamma ^{\kappa }}_{\mu \eta }-{\Gamma ^{\eta }}_{\mu \lambda }{\Gamma ^{\kappa }}_{\nu \eta }}$,

sendo ${\displaystyle \nabla _{v}\mathbf {e} _{\lambda }={\Gamma ^{\eta }}_{\nu \lambda }\mathbf {e} _{\eta }}$.^[3]

Comutadores e índices

Dado um quadrivetor genérico ${\displaystyle A}$, o tensor de Riemann surge da comutação da derivada covariante segunda desse quadrivetor, ou seja,^[4]

${\displaystyle [\nabla _{\mu },\nabla _{\nu }]A^{\rho }=\nabla _{\mu }\nabla _{\nu }A^{\rho }-\nabla _{\nu }\nabla _{\mu }A^{\rho }={R^{\rho }}_{\sigma \mu \nu }A^{\sigma }-{T^{\lambda }}_{\mu \nu }\nabla _{\lambda }A^{\rho }}$,

no qual ${\displaystyle {T^{\lambda }}_{\mu \nu }}$ é o tensor de torção.

Considerando o caso em que não há torção, isto é,

${\displaystyle [\nabla _{\mu },\nabla _{\nu }]A^{\rho }={R^{\rho }}_{\sigma \mu \nu }A^{\sigma }}$,

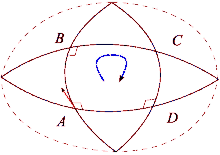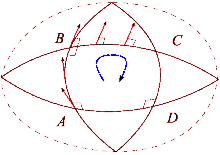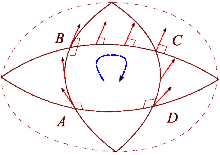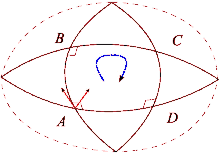
o tensor de Riemann expressa a diferença medida da curvatura da variedade ${\displaystyle M}$ quando o vetor ${\displaystyle A}$ é transportado do ponto ${\displaystyle p}$ para um ponto ${\displaystyle q}$, primeiramente ao longo de uma congruência, e depois seguindo outra congruência, ou vice-versa.^[5]

Versão covariante

O tensor métrico covariante ${\displaystyle g_{\rho \zeta }}$ pode se usado para abaixar um índice do tensor de Riemann, assim como o tensor contravariante ${\displaystyle g^{\rho \zeta }}$ pode levantar um índice. Assim, a versão completamente covariante do tensor de curvatura do tipo (0,4) é dada por

${\displaystyle R_{\rho \sigma \mu \nu }=g_{\rho \zeta }{R^{\zeta }}_{\sigma \mu \nu }.}$

Propriedades

Simetrias algébricas

O tensor de Riemann é antissimétrico nos dois últimos índices, ou seja,

${\displaystyle {R^{\rho }}_{\sigma \mu \nu }=-{R^{\rho }}_{\sigma \nu \mu }}$,

${\displaystyle R_{\rho \sigma \mu \nu }=-R_{\rho \sigma \nu \mu }}$.

Na sua forma completamente covariante, o tensor de Riemann é antissimétrico em relação à troca dos dois primeiros índices, isto é,

${\displaystyle R_{\rho \sigma \mu \nu }=-R_{\sigma \rho \mu \nu }}$,

e é simétrico em relação à troca do primeiro par de índices com o segundo:

${\displaystyle R_{\rho \sigma \mu \nu }=R_{\mu \nu \rho \sigma }}$.

Primeira identidade de Bianchi

Na ausência de torção, temos:

${\displaystyle R_{\rho \sigma \mu \nu }+R_{\rho \nu \sigma \mu }+R_{\rho \mu \nu \sigma }=0}$.

Esta relação também pode ser escrita mais como

${\displaystyle R_{\rho [\sigma \mu \nu ]}=0}$,

em que ${\displaystyle [\sigma \mu \nu ]}$ indica uma antissimetrização nos índices. Assim, deve-se efetuar uma soma sobre todas as permutações dos três últimos índices, com um sinal correspondente à paridade da permutação. Resultando em 6 termos, mas que podem ser acoplados em virtude das propriedades algébricas descritas acima.

Componentes independentes

Embora o tensor de Riemann tenha ${\displaystyle n^{4}}$ componentes, em que ${\displaystyle n}$ é a dimensão da variedade sobre qual o tensor é definido, as relações descritas anteriormente reduzem este número a ${\displaystyle {\frac {1}{12}}n^{2}(n^{2}-1)}$ componentes independentes. Para duas, três e quatro dimensões, o número de componentes independentes é respectivamente 1, 6 e 20.^[6]

Segunda identidade de Bianchi

A segunda identidade de Bianchi é parecida com a primeira, mas leva em consideração a derivada covariante do tensor de Riemann. Na ausência de torção, a identidade possui a seguinte forma:

${\displaystyle \nabla _{\lambda }R_{\rho \sigma \mu \nu }+\nabla _{\rho }R_{\sigma \lambda \mu \nu }+\nabla _{\sigma }R_{\lambda \rho \mu \nu }=0}$.

Essa igualdade pode ser escrita de forma mais concisa como^[4]

${\displaystyle \nabla _{[\lambda }R_{\rho \sigma ]\mu \nu }=0}$.

Tensor de curvatura de Ricci

O tensor de curvatura de Ricci é a contração do primeiro e terceiro índice do tensor de Riemann.

${\displaystyle \underbrace {\operatorname {R} _{ab}} _{\text{Ricci}}\equiv \underbrace {\operatorname {R} ^{c}{}_{acb}} _{\text{Riemann}}=g^{cd}\underbrace {\operatorname {R} _{cadb}} _{\text{Riemann}}}$

Referências