Função diferenciável

Em matemática, uma função diferenciável de uma variável real é uma função cuja derivada existe em cada ponto de seu domínio. Em outras palavras, o gráfico de uma função diferenciável tem uma reta tangente [en] não vertical [en] em cada ponto interior de seu domínio. Uma função diferenciável é suave (a função é bem aproximada localmente como uma função linear em cada ponto interior) e não contém nenhuma quebra, ângulo, ou cúspide [en].
Se x0 é um ponto interior no domínio de uma função f, então f é dita diferenciável em x0 se a derivada existe. Em outras palavras, o gráfico de f tem uma reta tangente não vertical no ponto (x0, f(x0)). f diz-se diferenciável em U se é diferenciável em cada ponto de U. f diz-se continuamente diferenciável se sua derivada também é uma função contínua sobre o domínio da função . De um modo geral, diz-se que f é da classe se suas primeiras derivadas existem e são contínuas no domínio da função .
Para uma função multivariável, como mostrado aqui, a diferenciabilidade dela é algo mais do que a existência das derivadas parciais dela.
Diferenciabilidade de funções reais de uma variável
Uma função , definida em um conjunto aberto , é dita diferenciável em um se a derivada
existe. Isso implica que a função é contínua em a.
Esta função f é dita diferenciável em U se for diferenciável em cada ponto de U. Neste caso, a derivada de f é, portanto, uma função de U em .
Uma função contínua não é necessariamente diferenciável, mas uma função diferenciável é necessariamente contínua (em todos os pontos onde é diferenciável) como mostrado abaixo (na seção Diferenciabilidade e continuidade). Diz-se que uma função é continuamente diferenciável se sua derivada também é uma função contínua; existem funções que são diferenciáveis, mas não continuamente diferenciáveis, (um exemplo é dado na seção Classes de diferenciabilidade).
Diferenciabilidade e continuidade


Se f é diferenciável em um ponto x0, então f também deve ser contínua em x0. Em particular, qualquer função diferenciável deve ser contínua em todos os pontos de seu domínio. O inverso não é válido: uma função contínua não precisa ser diferenciável. Por exemplo, uma função com dobra, cúspide [en] ou tangente vertical [en] pode ser contínua, mas não diferenciável no local da anomalia.
A maioria das funções que ocorrem na prática tem derivadas em todos os pontos ou em quase todos [en] os pontos. No entanto, um resultado de Stefan Banach afirma que o conjunto de funções que possuem uma derivada em algum ponto é um conjunto escasso no espaço de todas as funções contínuas.[1] Informalmente, isso significa que funções diferenciáveis são muito atípicas entre funções contínuas. O primeiro exemplo conhecido de uma função contínua em todos os lugares, mas diferenciável em nenhum lugar, é a função de Weierstrass.
Classes de diferenciabilidade
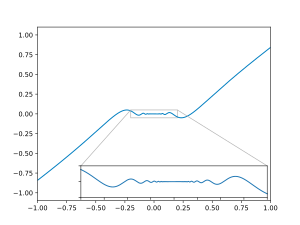
 Ver artigo principal: Suavidade
Ver artigo principal: SuavidadeUma função é dita continuamente diferenciável se a derivada existe e é ela própria uma função contínua. Embora a derivada de uma função diferenciável nunca tenha uma descontinuidade de salto [en], é possível que a derivada tenha uma descontinuidade essencial [en]. Por exemplo, a função
Da mesma forma como as funções contínuas são consideradas de classe , as funções continuamente diferenciáveis são às vezes consideradas de classe . Uma função é de classe se a primeira e a segunda derivada da função existem e são contínuas. De forma mais geral, diz-se que uma função é de classe se as primeiras derivadas todas existem e são contínuas. Se as derivadas existem para todos os inteiros positivos , a função é suave ou equivalente, de classe .
Diferenciabilidade em dimensões superiores
Uma função de várias variáveis reais [en] f: Rm → Rn é dita diferenciável em um ponto x0 se existe um mapa linear J: Rm → Rn tal que
Se uma função é diferenciável em x0, então todas as derivadas parciais existem em x0, e o mapa linear J é dado pela matriz jacobiana, uma matriz n × m neste caso. Uma formulação semelhante da derivada de dimensão superior é fornecida pelo lema do incremento fundamental [en] encontrado no cálculo de variável única.
Se todas as derivadas parciais de uma função existem na vizinhança de um ponto x0 e são contínuas no ponto x0, então a função é diferenciável naquele ponto x0.
Entretanto, a existência das derivadas parciais (ou mesmo de todas as derivadas direcionais) não garante que uma função seja diferenciável em um ponto. Por exemplo, a função f: R2 → R definida por
não é diferenciável em (0, 0), mas todas as derivadas parciais e direcionais existem neste ponto. Para um exemplo contínuo, a função
não é diferenciável em (0, 0), mas novamente todas as derivadas parciais e direcionais existem.
Diferenciabilidade em análise complexa
 Ver artigo principal: Função holomorfa
Ver artigo principal: Função holomorfaNa análise complexa, a diferenciabilidade complexa é definida usando a mesma definição que as funções reais de variável única. Isso é permitido pela possibilidade de dividir números complexos. Assim, uma função é dita diferenciável em quando
Embora essa definição pareça semelhante à diferenciabilidade de funções reais de variável única, é, no entanto, uma condição mais restritiva. Uma função , que é diferenciável complexa em um ponto é automaticamente diferenciável nesse ponto, quando vista como uma função . Isso ocorre porque a diferenciabilidade complexa implica que
No entanto, uma função pode ser diferenciável como uma função multivariável, embora não seja diferenciável complexa. Por exemplo, é diferenciável em cada ponto, visto como a função real bivariável , mas não é diferenciável em nenhum ponto porque o limite não existe (por exemplo, isso depende do ângulo de aproximação).
Qualquer função que é complexamente diferenciável na vizinhança de um ponto é chamada de holomorfa naquele ponto. Tal função é necessariamente infinitamente diferenciável e, de fato, analítica.
Funções diferenciáveis em variedades
Se M é uma variedade diferenciável, uma função real ou de valor complexo f em M é dita diferenciável em um ponto p se for diferenciável em relação a algum (ou qualquer) gráfico de coordenadas definido em torno de p. Se M e N são variedades diferenciáveis, uma função f: M → N é dita diferenciável em um ponto p se for diferenciável em relação a algum (ou qualquer) gráfico de coordenadas definido em torno de p e f(p).
Ver também
- Generalizações da derivada [en]
- Programação diferenciável [en]
- Semidiferenciabilidade [en]
Referências
- ↑ Banach, S. (1931). «Über die Baire'sche kategorie gewisser funktionenmengen». Studia mathematica. 3 (1): 174 – 179. doi:10.4064/sm-3-1-174-179
 . Citado por Hewitt, E.; Stromberg, K. (1963). Real and abstract analysis (em inglês). [S.l.]: Springer-Verlag. Theorem 17.8
. Citado por Hewitt, E.; Stromberg, K. (1963). Real and abstract analysis (em inglês). [S.l.]: Springer-Verlag. Theorem 17.8



















































