Campo vettoriale

In matematica, un campo vettoriale su uno spazio euclideo è una costruzione del calcolo vettoriale che associa a ogni punto di una regione di uno spazio euclideo un vettore dello spazio stesso.

Un campo vettoriale tangente su una varietà differenziabile è una funzione che associa ad ogni punto della varietà un vettore dello spazio tangente in quel punto alla varietà. Il teorema di Helmholtz è fondamentale per questi oggetti, in quanto afferma che la conoscenza della divergenza e del rotore sono necessari e sufficienti alla conoscenza del campo stesso.

Un campo vettoriale sul piano si può rappresentare visivamente pensando ad una distribuzione nel piano di vettori bidimensionali, in modo che il vettore immagine del punto ${\displaystyle x}$ abbia l'origine in ${\displaystyle x}$ stesso (eventualmente riscalato per una migliore resa visiva come in figura). In modo analogo, si possono visualizzare campi vettoriali su superfici o nello spazio tridimensionale.

Descrizione

Definizione

Dato un insieme aperto e connesso ${\displaystyle X}$ contenuto in ${\displaystyle \mathbb {R} ^{n}}$, un campo vettoriale è una funzione:

${\displaystyle F:X\rightarrow \mathbb {R} ^{n}}$

alla quale si richiede generalmente di essere continua o differenziabile per un certo numero di volte. In quanto funzione, ad esempio, nel caso di superficie, si può scrivere:

${\displaystyle {\mathbf {v} }=F(x,y,t)}$ ovvero ad ogni punto della superficie è associato un vettore

mentre nel caso di spazio:

${\displaystyle {\mathbf {v} }=F(x,y,z,t)}$ ovvero ad ogni punto dello spazio è associato un vettore

Linee di flusso

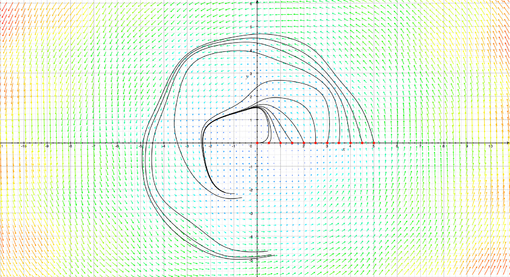
Le linee di flusso sono intuitivamente delle curve che seguono in ogni loro punto le direzioni individuate dal campo vettoriale con velocità data dall'ampiezza dei vettori del campo. Interpretando il campo vettoriale come un campo di velocità di un fluido, queste linee rappresentano le traiettorie di ogni singola particella. Formalmente, una linea di flusso passante per un punto ${\displaystyle x}$ è una curva differenziabile:

${\displaystyle \phi :(-R,R)\to X}$

definita per qualche ${\displaystyle R}$ positivo, tale che

${\displaystyle \phi (0)=x}$ e ${\displaystyle \phi '(t)=F(\phi (t))}$ per ogni ${\displaystyle t}$.

Se il campo è sufficientemente "regolare" (ad esempio, se ${\displaystyle F}$ è differenziabile o almeno lipschitziano), per ogni punto passa esattamente una linea di flusso. Questo perché una linea di flusso è soluzione di un problema di Cauchy, la cui esistenza e unicità è garantita dal teorema di esistenza e unicità per un problema di Cauchy.

Flusso di fase associato ad un campo vettoriale

Una linea di flusso è definita su un intervallo aperto ${\displaystyle (-R,R)}$, ma non è necessariamente definita su tutta la retta reale. In un campo vettoriale tale che tutte le linee di flusso sono definite sull'intera retta reale, è possibile definire una applicazione

${\displaystyle \Phi :\mathbb {R} \times X\to X}$

che associa ad una coppia ${\displaystyle (t,x)}$ - data da un tempo e un punto dello spazio delle fasi - il punto di arrivo che si ottiene seguendo la linea di flusso che parte da ${\displaystyle x}$ per un tempo ${\displaystyle t}$ a partire dal punto ${\displaystyle x}$. Tale applicazione è il flusso associato al campo vettoriale e si è soliti scrivere ${\displaystyle \Phi _{t}(x)}$ per indicare l'immagine della coppia ${\displaystyle (t,x)}$.

Formalmente il flusso associato al campo vettoriale ${\displaystyle F}$ è individuato da una famiglia di applicazioni

${\displaystyle \{\Phi _{t}:X\to X\,|\,t\in \mathbb {R} \}}$

che verificano le condizioni:

${\displaystyle {\begin{cases}\Phi _{0}(x)=x\\\left.{\frac {d}{dt}}\Phi _{t}(x)\right|_{t=t_{0}}=F(\Phi _{t_{0}}(x))\end{cases}}}$

per ogni ${\displaystyle x}$ e per ogni tempo ${\displaystyle t_{0}}$.

Il flusso è un "gruppo ad un parametro": è un gruppo perché soddisfa le proprietà seguenti

• ${\displaystyle \Phi _{0}={\mbox{Id}}_{X}}$
• ${\displaystyle \Phi _{s+t}=\Phi _{s}\circ \Phi _{t}}$

e definisce un'azione di ${\displaystyle \mathbb {R} }$ su ${\displaystyle X}$. Le proprietà di gruppo ci dicono informalmente che l'evoluzione dello spazio indotta dal flusso per un tempo ${\displaystyle 0}$ corrisponde a lasciare tutto com'è, e che l'evoluzione per un tempo ${\displaystyle s+t}$ equivale all'applicazione successiva di due evoluzioni per tempi ${\displaystyle s}$ e ${\displaystyle t}$.

Punti critici

Definizione

Un punto critico o punto singolare per un campo vettoriale è un punto in cui il campo si annulla, o in cui non è definito perché tende a infinito (similmente a quanto accade per i poli). Generalmente, si suppone che il campo sia sufficientemente regolare, così che i punti critici sono isolati.

I punti critici devono il proprio nome al ruolo "speciale" che rivestono all'interno del campo vettoriale. Nell'intorno di qualsiasi punto non critico la struttura topologica del campo vettoriale è sempre la stessa: il campo ristretto ad un intorno piccolo del punto è diffeomorfo ad un campo costante (che associa ad ogni punto lo stesso vettore non nullo), le cui linee di flusso sono quindi rette parallele, come stabilito dal teorema della scatola di flusso. I punti critici invece hanno una casistica molto più ricca.

Topologia

Le possibili strutture topologiche del campo in un intorno del punto critico isolato si possono classificare associando ai punti critici un numero intero chiamato indice.

Il tipo ed il numero complessivo dei punti critici di un campo vettoriale sono anche legati alla struttura topologica globale del dominio su cui il campo è definito. Questo legame è stabilito dal teorema di Poincaré-Hopf il quale afferma che se il campo vettoriale è definito su una varietà differenziabile compatta allora la somma degli indici dei suoi punti critici è uguale alla caratteristica di Eulero della varietà.

Varietà pettinabili

Una varietà differenziale è pettinabile se ammette un campo vettoriale (sufficientemente regolare) mai nullo. Per il teorema di Poincaré-Hopf menzionato sopra, una varietà compatta pettinabile deve avere caratteristica di Eulero zero. Per questo motivo, la sfera non è pettinabile: questo enunciato è il teorema della sfera pelosa.

D'altro canto, il toro e la bottiglia di Klein sono superfici con caratteristica di Eulero zero, e sono pettinabili.

Applicazioni

I campi vettoriali si incontrano sia nella matematica pura che in quella applicata:

• In fisica sono utilizzati per modellizzare le grandezze vettoriali distribuite con continuità nello spazio, grandezze caratterizzate da una intensità e da una direzione, per esempio spostamento, velocità e accelerazione di un fluido, campi di forze, come nel caso di un campo gravitazionale, elettrico o magnetico, i venti in meteorologia ecc.

• Nell'analisi e nello studio dei sistemi dinamici i campi vettoriali sono intimamente connessi con le equazioni differenziali.

• Nella topologia differenziale si studiano le connessioni tra le proprietà dei campi vettoriali continui su una varietà differenziabile e la struttura topologica della varietà. Un esempio è il teorema della palla pelosa che stabilisce che su una sfera (e su qualunque superficie diffeomorfa ad una sfera) non è possibile definire un campo vettoriale continuo e mai nullo.

Esempi

Campo vettoriale gradiente

Data una funzione differenziabile su ${\displaystyle X\subset \mathbb {R} ^{n}}$

${\displaystyle f:X\rightarrow \mathbb {R} }$

il campo gradiente di ${\displaystyle f}$ è il campo vettoriale che associa ad ogni ${\displaystyle x}$ in ${\displaystyle X}$ il vettore

${\displaystyle F(x):=\nabla f(x)}$

dato dal gradiente di ${\displaystyle f}$ in ${\displaystyle x}$.

Un campo gradiente è conservativo, cioè il rotore è ovunque nullo.

Le linee di flusso di un campo gradiente associato ad una funzione scalare ${\displaystyle f}$ sono ovunque ortogonali alle superfici di livello di ${\displaystyle f}$, cioè alle ipersuperfici date dall'equazione cartesiana ${\displaystyle f(x)=c}$ al variare di ${\displaystyle c}$ in ${\displaystyle \mathbb {R} }$.

Campo vettoriale hamiltoniano

Data una funzione differenziabile su un aperto ${\displaystyle X}$ del piano cartesiano ${\displaystyle \mathbb {R} ^{2}}$:

${\displaystyle H:X\rightarrow \mathbb {R} ^{2}}$

il campo Hamiltoniano di ${\displaystyle H}$ è il campo vettoriale che associa ad un punto ${\displaystyle (x,y)}$ in ${\displaystyle X}$ il vettore

${\displaystyle F(x,y)=(H_{y}(x,y),-H_{x}(x,y))}$

dove ${\displaystyle H_{x}}$ e ${\displaystyle H_{y}}$ denotano le derivate parziali di ${\displaystyle H}$.

La funzione scalare ${\displaystyle H}$ che genera il campo Hamiltoniano si chiama Hamiltoniana.

Bibliografia

• (EN) J. H. Hubbard e B. B. Hubbard, Vector calculus, linear algebra, and differential forms. A unified approach, Upper Saddle River, NJ, Prentice Hall, 1999, ISBN 0-13-657446-7.
• (EN) Frank Warner, Foundations of differentiable manifolds and Lie groups, New York-Berlin, Springer-Verlag, 1983 [1971], ISBN 0-387-90894-3.
• (EN) William Boothby, An introduction to differentiable manifolds and Riemannian geometry, Pure and Applied Mathematics, volume 120, second, Orlando, FL, Academic Press, 1986, ISBN 0-12-116053-X.
• (EN) Galbis, Antonio & Maestre, Manuel, Vector Analysis Versus Vector Calculus, Springer, 2012, p. 12, ISBN 978-1-4614-2199-3.
• (EN) Tu, Loring W., Vector fields, in An Introduction to Manifolds, Springer, 2010, p. 149, ISBN 978-1-4419-7399-3.
• (EN) Dawber, P.G., Vectors and Vector Operators, CRC Press, 1987, p. 29, ISBN 978-0-85274-585-4.

Voci correlate

• Campo vettoriale hamiltoniano
• Divergenza
• Gradiente
• Rotore (matematica)
• Spazio tangente
• Teorema della palla pelosa
• Teorema di Helmholtz
• Varietà differenziabile

Altri progetti

• Wikizionario contiene il lemma di dizionario «campo vettoriale»
• Wikimedia Commons contiene immagini o altri file sul campo vettoriale

Collegamenti esterni

• (EN) vector field, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.
• (EN) Eric W. Weisstein, Campo vettoriale, su MathWorld, Wolfram Research.
• (EN) Campo vettoriale, in PlanetMath.
• (EN) Paul Falstad, Simulazione Campi Vettoriali 2D Applicazione Java per la visualizzazione di campi vettoriali 2D
• (EN) Paul Falstad, Simulazione Campi Vettoriali 3D Applicazione Java per la visualizzazione di campi vettoriali 3D

Controllo di autorità	GND (DE) 4139571-2 · J9U (EN, HE) 987007534278505171