Approssimazione di Kochański

In matematica, l'approssimazione di Kochański consente di ottenere un valore approssimato di π a partire da una particolare costruzione geometrica. Prende il nome dal religioso gesuita e matematico polacco Adam Adamandy Kochański, che per primo la propose nel suo trattato Observationes Cyclometricæ ad facilitandam Praxin accommodatae del 1685, dedicato al problema della rettificazione della circonferenza^[1][2].

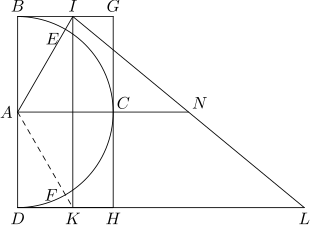
La costruzione che segue è la versione originale che compare nel trattato di Kochański e fornisce una soluzione al problema della rettificazione di una circonferenza unitaria, attraverso la determinazione geometrica di un segmento di lunghezza approssimativamente pari a π (cioè la semicirconferenza di un cerchio unitario).

Si costruisca una semicirconferenza ${\displaystyle BCD}$ di raggio unitario centrata in ${\displaystyle A}$ e la si inscriva nel rettangolo ${\displaystyle BGHD}$. Si tracci il raggio ${\displaystyle AE}$ che forma rispetto al raggio ${\displaystyle AC}$ un angolo di ${\displaystyle 60^{\circ }}$, e lo si prolunghi fino a intercettare il segmento ${\displaystyle BG}$ nel punto ${\displaystyle I}$. Si prolunghi infine ${\displaystyle DH}$ di un segmento ${\displaystyle HL}$ di lunghezza pari al diametro della semicirconferenza.

La lunghezza del segmento ${\displaystyle IL}$ è una approssimazione di π: infatti, riguardando ${\displaystyle IL}$ come l'ipotenusa del triangolo rettangolo ${\displaystyle IKL}$ e applicando il teorema di Pitagora si ha che:^[2]

${\displaystyle {\begin{aligned}IL&={\sqrt {IK^{2}+KL^{2}}}={\sqrt {2^{2}+\left[\left(1-\tan {30^{\circ }}\right)+2\right]^{2}}}\\&={\sqrt {4+\left(3-{\frac {1}{3}}{\sqrt {3}}\right)^{2}}}={\sqrt {{\frac {40}{3}}-2{\sqrt {3}}}}=3,141533...\approx \pi .\end{aligned}}}$

Si costruisca una circonferenza di raggio unitario centrata in ${\displaystyle O}$, e si definisca un sistema di riferimento con l'asse delle ordinate passante per il diametro verticale e l'origine posta nel punto ${\displaystyle A}$. Si tracci ora il cerchio centrato in ${\displaystyle A}$ e di raggio unitario; esso intersecherà il primo cerchio nel punto ${\displaystyle C\left(-{\frac {\sqrt {3}}{2}},{\frac {1}{2}}\right)}$. Si tracci il cerchio centrato in ${\displaystyle C}$ di raggio unitario, che intersecherà il secondo cerchio nel punto ${\displaystyle D\left(-{\frac {\sqrt {3}}{2}},-{\frac {1}{2}}\right)}$. Il segmento che congiunge ${\displaystyle O}$ e ${\displaystyle D}$ interseca l'asse delle ascisse passante per ${\displaystyle A}$ nel punto ${\displaystyle E\left(-{\frac {\sqrt {3}}{3}},0\right)}$. Si costruisca infine il punto ${\displaystyle F\left(3-{\frac {\sqrt {3}}{3}},0\right)}$ in modo che si trovi a distanza 3 da ${\displaystyle D}$ nella direzione positiva delle ascisse.

La lunghezza del segmento ${\displaystyle BF}$ ottenuto da questa costruzione geometrica è una approssimazione del valore di π, corretta fino alla quarta cifra decimale. Infatti, osservando ${\displaystyle BF}$ come l'ipotenusa del triangolo rettangolo ${\displaystyle BAF}$ e applicando il teorema di Pitagora si ha:

${\displaystyle BF={\sqrt {2^{2}+\left(3-{\frac {1}{3}}{\sqrt {3}}\right)^{2}}}={\sqrt {{\frac {40}{3}}-2{\sqrt {3}}}}=3,141533...\approx \pi .}$^[3][4]

• Arbelo
• Archimede
• Cerchio
• Circonferenza

• Wikimedia Commons contiene immagini o altri file su approssimazione di Kochański

• (EN) Eric W. Weisstein, Approssimazione di Kochański, su MathWorld, Wolfram Research.

Portale Matematica: accedi alle voci di Wikipedia che trattano di matematica