Polárkoordináta-rendszer

A matematikában és a geodéziában a polárkoordináta-rendszer olyan kétdimenziós koordináta-rendszer, mely a sík minden pontját egy szög és egy távolság adattal látja el. Tulajdonképpen itt a sík egy paraméterezéséről beszélhetünk. A polárkoordináták a sík egy kitüntetett pontjától mért távolságból és egy, a ponton átmenő, vektorosan definiált egyenestől mért irányszögből állnak. Konkrétan a hozzárendelés, mely a sík derékszögű koordináta-rendszerben megadott (x,y) koordinátájú pontjait ellátja polárkoordinátákkal a következő kapcsolatban van a derékszögű koordinátákkal:

${\displaystyle \left\{{\begin{matrix}x=r\cdot \cos \varphi \\y=r\cdot \sin \varphi \end{matrix}}\right.}$

ahol r a sík P(x,y) pontjának origótól mért távolsága (nemnegatív szám), φ pedig az x tengely és az OP szakasz irányított szögtávolsága (ez radiánban 0 és 2π közötti érték, fokban 0° és 360° közötti). A koordinátavonalakat ebben a rendszerben egyfelől azon pontok alkotják, melyek mentén a φ koordináta állandó, vagyis az origóból induló félegyenesek, másrészt azok, amelyek mentén r állandó, vagyis az origó középpontú körök. A matematikában a szög előjeles, a pozitív forgásirány az óramutató járásával ellentétes irány. A geodéziában az óramutató járása szerinti irány a pozitív. A polárkoordináta-rendszerek a derékszögű görbe vonalú koordináta-rendszerek speciális esetei.

A polárkoordináta rendszert olyankor célszerű használni az elterjedtebb Descartes-féle derékszögű koordináta-rendszerrel szemben, ha a pontok helyének megadása egyszerűbb távolságokkal és szögekkel, mint két egymásra merőleges szakasz hosszával. Ilyen terület például a geodézia, ahol a derékszögű koordináta-rendszer az ortogonális mérésnek felel meg, amit mérőszalaggal és derékszögprizmával végeznek. A pontos szögmérő műszerek (teodolit) elterjedésével a poláris mérés került előtérbe, amely távolság- és szögmérési adatokból számít koordinátákat.

Definíció

Amikor polárkoordinátával jellemezzük a sík egy P pontját, akkor a pontot két adatával adjuk meg. Ehhez először rögzítenünk kell egy középpontot, a pólust (vagy a derékszögű koordináta rendszerrel történő összevetésben az origót), továbbá egy origó végpontú félegyenest, mely a kezdő irányt rögzíti. A polárkoordináták közül a távolsági adat a kezdőponttól adott távolságban lévő pontok halmazát, azaz egy kört határoz meg. Az irányszög a kezdő iránytól adott szögben látszó pontok halmazát, azaz egy félegyenest határoz meg. A körív és a félegyenes metszéspontja lesz a polárkoordinátákkal megadott pont.

Az r-rel jelölt koordináta, a sugár, a pont origótól mért távolsága, néha R-rel vagy ρ-val is jelölik. Ha O jelöli az origót és OA jelöli a kezdő irány félegyenesét, akkor a P pont φ koordinátája nem más, mint az OP félegyenes és az OA félegyenes irányított szöge. Az irányítás azt jelenti, hogy a szöget az OA félegyenestől az óramutató járásával ellentétes körüljárással mérjük. A szöget gyakran még θ-val, α-val és még sok mással is jelölik. A szög megadása az SI-nek megfelelő módon radiánban történik, de sokszor természetesen fokokat is használnak.

Átváltás a derékszögű és polárkoordináták között

Világos, hogy ha az r és a φ adott a sík egy P pontjára vonatkoztatva, akkor az szögfüggvények 90°-nál nagyobb szögekre való kiterjesztésének definíciója folytán a derékszögű koordinátákba való átváltás a következő. Ha a kezdő irányt az x tengelynek fogjuk fel és ennek origó körüli +90°-os elforgatottját az y tengelynek, akkor a derékszögű koordináták:

${\displaystyle x=r\cdot \cos \varphi \,}$

${\displaystyle y=r\cdot \sin \varphi \,}$

Ha a derékszögű koordináták az adottak, akkor az x és y adatokból a távolságot például a Pitagorasz-tétellel számíthatjuk:

${\displaystyle r={\sqrt {x^{2}+y^{2}}}\,}$

A φ értékéhez a szögfüggvényértékek visszakeresésének módszerével juthatunk. Itt természetesen vigyázni kell arra – mint minden esetben, amikor trigonometrikus értékekből következtetünk vissza szögértékre –, hogy helyes szöget adjon vissza a számítás. Ehhez a következőket kell szem előtt tartani.

• ${\displaystyle r}$ = 0 esetén φ a polárkoordináta-rendszerben határozatlan, azaz bármely valós érték alkalmas lenne az origó szögének jellemzésére, hiszen ez az érték egyáltalán nem jellemzője az origónak
• ${\displaystyle r}$ ≠ 0 esetén ahhoz, hogy a φ polárkoordinátára egyetlen értéket kapjunk, 2π hosszúságú intervallumra kell korlátozódnunk. A szokásos tartományok [0, 2π) vagy (-π, π].

[0, 2π) illetve [0, 360°) intervallumba eső szög esetén

A [0, 2π) tartományban az inverz szögfüggvények (arkusz függvények) segítségével kapjuk meg φ-t:

${\displaystyle \varphi ={\begin{cases}\mathrm {arctg} ({\frac {y}{x}})&{\mbox{ha }}x>0~{\acute {e}}s~y\geq 0\\\mathrm {arctg} ({\frac {y}{x}})+2\pi &{\mbox{ha }}x>0~{\acute {e}}s~y<0\\\mathrm {arctg} ({\frac {y}{x}})+\pi &{\mbox{ha }}x<0\\{\frac {\pi }{2}}&{\mbox{ha }}x=0~{\acute {e}}s~y>0\\{\frac {3\pi }{2}}&{\mbox{ha }}x=0~{\acute {e}}s~y<0\end{cases}}}$

Az árkusz koszinusz leegyszerűsíti az esetszétválasztást:

${\displaystyle \varphi '={\begin{cases}\arccos {\frac {x}{r}}&\mathrm {ha} \ y\geq 0\\2\pi -\arccos {\frac {x}{r}}&\mathrm {ha} \ y<0\end{cases}}}$

(−π, π] illetve (−180°,180°] intervallumba eső szög esetén

A (-π, π] tartományban pedig a φ polárszög értéke:

${\displaystyle \varphi ={\begin{cases}\mathrm {arctg} ({\frac {y}{x}})&{\mbox{ha }}x>0\\\mathrm {arctg} ({\frac {y}{x}})+\pi &{\mbox{ha }}x<0~{\acute {e}}s~y\geq 0\\\mathrm {arctg} ({\frac {y}{x}})-\pi &{\mbox{ha }}x<0~{\acute {e}}s~y<0\\{\frac {\pi }{2}}&{\mbox{ha }}x=0~{\acute {e}}s~y>0\\-{\frac {\pi }{2}}&{\mbox{ha }}x=0~{\acute {e}}s~y<0\end{cases}}}$

Egyes programozási nyelvek és alkalmazások tartalmaznak egy arctan2(x, y) függvényt, ami figyelembe veszi a fenti esetszétválasztást, és tetszőleges ${\displaystyle x,y}$ esetén képes φ értéket számolni.

Ugyanezt az eredményt kapjuk, ha az ${\displaystyle x,y}$ koordinátájú pontot azonosítjuk a ${\displaystyle z=x+\mathrm {i} y}$ komplex számmal, és az

${\displaystyle \varphi =\arg(z)}$

szöget az ${\displaystyle \arg }$ argumentumfüggvénnyel számoljuk.

Az árkusz koszinusz segítségével az esetszétválasztás egyszerűsíthető:

${\displaystyle \varphi ={\begin{cases}+\arccos {\frac {x}{r}}&\mathrm {ha} \ y\geq 0\\-\arccos {\frac {x}{r}}&\mathrm {ha} \ y<0\end{cases}}}$

A középponti és a kerületi szögek tételéből tudjuk, hogy egy körben a középponti szög kétszer akkora, mint a hozzá tartozó kerületi szög. Így a ${\displaystyle \varphi }$ szög kiszámítása az árkusz tangens használatával is egyszerűsíthető:

${\displaystyle \varphi ={\begin{cases}2\operatorname {arctg} {\frac {y}{r+x}}&\mathrm {ha} \ r+x\neq 0\\\pi &\mathrm {ha} \ r+x=0\end{cases}}}$

A szög eltolása

Egyes alkalmazásokban más szögtartományokat használnak. Legyen ${\displaystyle \varphi _{\text{min}}=0}$ az alsó határ! Ekkor az

${\displaystyle \phi =\varphi -2\pi \cdot {\bigl \lfloor }{\frac {\varphi -\varphi _{\text{min}}}{2\pi }}{\bigr \rfloor }}$

egyenlet a ${\displaystyle \varphi }$ szöget a kívánt intervallumba transzformálja, így az is teljesül, hogy ${\displaystyle \phi \in \left[\varphi _{\text{min}},\,\varphi _{\text{min}}+2\pi \right)}$. Itt ${\displaystyle x\mapsto \lfloor x\rfloor }$ az alsó egészrész, vagyis ${\displaystyle \lfloor x\rfloor }$ minden ${\displaystyle x}$ valós számhoz a legnagyobb egész számot rendeli, ami nem nagyobb, mint ${\displaystyle x}$.

Koordinátavonalak

Egy ${\displaystyle (r_{0};\varphi _{0})}$ koordinátákkal adott pont koordinátavonalai:

${\displaystyle {\vec {k}}_{1}(r)={\begin{pmatrix}r\cos \varphi _{0}\\r\sin \varphi _{0}\end{pmatrix}},r\in [0,\infty [}$ és

${\displaystyle {\vec {k}}_{2}(\varphi )={\begin{pmatrix}r_{0}\cos \varphi \\r_{0}\sin \varphi \end{pmatrix}},\varphi \in [0,2\pi [}$,

azaz egy, a középpontból kiinduló félegyenes, és egy origó körüli ${\displaystyle r_{0}}$ sugarú kör.

Példák polárkoordinátákra

Egyes algebrai görbék polárkoordinátás egyenletekkel definiálhatók. Sok esetben az ilyen egyenletek egyszerűen az ${\displaystyle r}$ sugarat θ függvényében adják meg. Az eredményül kapott görbe pontjait ${\displaystyle (r(\vartheta ),\vartheta )}$ alakban kapjuk meg és a görbét ${\displaystyle r}$ polárkoordinátás függvény grafikonjának tekinthetjük.

A szimmetria különböző estei az ${\displaystyle r}$ függvényből vezethetők le. Ha ${\displaystyle r(-\vartheta )}$ = ${\displaystyle r(\vartheta )}$, akkor a görbe szimmetrikus a (0°/180°) egyenesre, ha ${\displaystyle r(\pi -\vartheta )}$ = ${\displaystyle r(\vartheta )}$, akkor a függőleges (90°/270°) egyenesre szimmetrikus és ha ${\displaystyle r(\vartheta -\alpha )}$ = ${\displaystyle r(\vartheta )}$, akkor a görbe centrálisan szimmetrikus az origóra.

Bizonyos görbék függvénye sokkal egyszerűbben írható fel polárkoordináták segítségével, mint derékszögű koordinátákkal. Az ismertebbek közé tartozik az arkhimédészi spirál, a lemniszkáta, a Pascal-féle csigagörbe és a kardioid.

Kör

Az (${\displaystyle r}$₀, φ) középpontú és ${\displaystyle a}$ sugarú kör általános egyenlete

${\displaystyle r^{2}-2rr_{0}\cos(\vartheta -\varphi )+r_{0}^{2}=a^{2}.\,}$

Ez különböző módon egyszerűbbé tehető, hogy egyes speciális eseteknek megfeleljen, például ez az egyenlet

${\displaystyle r(\vartheta )=a\,}$

olyan ${\displaystyle a}$ sugarú kört ír le, melynek középpontja a pólusban van.

Egyenes

Sugárirányú egyenesek (vagyis, amelyek a póluson átmennek) egyenlete:

${\displaystyle \vartheta =\varphi \,}$,

ahol φ az egyenes szöge, azaz φ = arctan ${\displaystyle m}$, ahol ${\displaystyle m}$ az egyenes meredeksége (iránytangense) derékszögű koordináta-rendszerben. Nem sugárirányú egyenes egyenlete, mely a sugárirányú ${\displaystyle \vartheta }$ = φ egyenletű egyenesre merőleges és azt a (${\displaystyle r}$₀, φ) pontban metszi:

${\displaystyle r(\vartheta )={r_{0}}\sec(\vartheta -\varphi ).\,}$

Arkhimédészi spirál

Az arkhimédészi spirál egy Arkhimédész által felfedezett híres spirális görbe, melyet szintén le lehet írni egyszerű polárkoordinátás egyenlettel:

${\displaystyle r(\vartheta )=a+b\vartheta .\,}$

Az a paraméter változtatásával megfordul a spirális, a b viszont a spirális egy sugárhoz tartozó pontjainak távolságát adja meg, ami egy spirálisnál állandó érték. Az arkhimédészi spirálnak két ága van, az egyikre θ > 0, a másikra θ < 0. A két ág simán csatlakozik egymáshoz a pólusban. Az egyik ág tükörképe a 90°/270° egyenesre, mint tükörtengelyre a másik ágat adja. Ez a görbe az egyik első görbe volt a kúpszeletek után, mely a matematikai értekezésekben például szolgált a polárkoordinátás leírásra.

Kúpszeletek

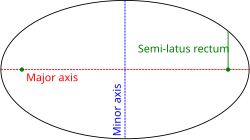
A kúpszelet polárkoordinátás egyenlete, ha a pólusban van az egyik fókusza és a másik valahol a 0°-os sugáron (így a főtengelye a poláris tengelyen fekszik):

${\displaystyle r={\ell \over {1+e\cos \vartheta }}}$

ahol e az excentricitás, és ${\displaystyle \ell }$ a semi-latus rectum (a fókuszból a főtengelyre a görbéig húzott egyenes szakasz hossza, ld. az ábrát). Ha e > 1, akkor az egyenlet hiperbolát definiál, ha e = 1, akkor a parabola egyenlete, míg e < 1 esetén a görbe ellipszis. Speciális eset az e = 0 az utóbbinál, amikor is az ellipszis ${\displaystyle \ell }$ sugarú körré fajul.

Komplex szám trigonometrikus alakja

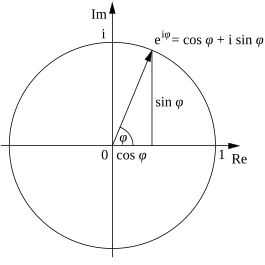
Minden komplex szám felfogható úgy, hogy az egy pont a komplex síkon, és így kifejezhető, mint egy derékszögű koordináta-rendszer egy pontja, vagy egy pont a polárkoordináta rendszeren. Derékszögű koordináta-rendszerben egy z szám így írható fel:

${\displaystyle z=x+iy\,}$

ahol i a képzetes egység, vagy polárkoordinátás alakba átírva:

${\displaystyle z=r\cdot (\cos \vartheta +i\sin \vartheta )}$

és innen

${\displaystyle z=re^{i\vartheta }\,}$

ahol e az Euler-féle szám, melyek azonosak az Euler-formula értelmében.

(Megjegyzendő, hogy ez a képlet ugyanúgy, mint minden más összefüggés, mely szögek hatványait tartalmazza, feltételezi, hogy a szögek radiánban vannak megadva.) A komplex számok derékszögű és polárkoordinátás alakjai közötti konverzió a fentebb leírt szabályok szerint történik.

A komplex számok szorzása, osztása és hatványozása általában sokkal egyszerűbb a poláris alakkal, mint a derékszögű változattal. A hatványozás szabályai szerint

• A szorzás:

${\displaystyle r_{0}e^{i\vartheta _{0}}\cdot r_{1}e^{i\vartheta _{1}}=r_{0}r_{1}e^{i(\vartheta _{0}+\vartheta _{1})}\,}$

• Az osztás:

${\displaystyle {\frac {r_{0}e^{i\vartheta _{0}}}{r_{1}e^{i\vartheta _{1}}}}={\frac {r_{0}}{r_{1}}}e^{i(\vartheta _{0}-\vartheta _{1})}\,}$

• A hatványozás (De Moivre-képlet):

${\displaystyle (re^{i\vartheta })^{n}=r^{n}e^{in\vartheta }\,}$

Polárkoordináta-transzformáció az analízisben

Polárkoordináta-transzformációt gyakran alkalmaznak olyan kétváltozós függvények esetén, melyek valamilyen középpontos szimmetriát mutatnak. Ekkor az D &sunbe; R × R halmazon értelmezett

${\displaystyle f:D\to \mathbf {R} ;\;(x,y)\mapsto f(x,y)\,}$

függvény helyett az

${\displaystyle (f\circ G)(r,\varphi )=f(r\cdot \cos \varphi ,r\cdot \sin \varphi )}$

függvényt vizsgálják, ahol a

${\displaystyle G:[0,+\infty )\times [0,2\pi );\quad (r,\varphi )\mapsto (r\cdot \cos \varphi ,r\cdot \sin \varphi )}$

leképezés a polártranszformáló függvény.

Megjegyzendő, hogy G csak majdnem mindenhol injektív. G legbővebb injektivitási tartománya a

${\displaystyle (0,+\infty )\times [0,2\pi )\,}$

Folytonosság, határérték

Kétváltozós függvény origóbeli határértékének létezését polárkoordinátákban a következőképpen mutathatjuk ki. Ha f kétváltozós függvény és A valós szám, akkor

${\displaystyle \exists \lim \limits _{0}f=A\quad \Leftrightarrow \quad \forall (r_{n},\varphi _{n})\in (\mathrm {Dom} (f\circ G)\setminus \{0\}\times [0,2\pi ))^{\mathbf {Z} ^{+}}\quad (\;\exists \lim(r_{n})=0\quad \Rightarrow \quad \exists \lim(f(G(r_{n},\varphi _{n})))=A\;)}$

Például az

${\displaystyle f(x,y)={\frac {xy^{2}}{x^{2}+y^{2}}}\,}$

függvénynek létezik az origóban határértéke, mert az x = r ${\displaystyle \cdot }$ cos(φ), y = r ${\displaystyle \cdot }$ sin(φ) helyettesítéssel:

${\displaystyle f(x(r,\varphi ),y(r,\varphi ))={\frac {r^{3}\cos(\varphi )\sin ^{2}(\varphi )}{r^{2}}}=r\cos(\varphi )\sin ^{2}(\varphi )}$

amely (0-hoz tartó) ${\displaystyle \cdot }$ (korlátos) alakú és így a 0-hoz tart. Míg az

${\displaystyle f(x,y)={\frac {xy}{x^{2}+y^{2}}}\,}$

függvénynek nem létezik az origóban határértéke, helyettesítve az

${\displaystyle f(x(r,\varphi ),y(r,\varphi ))={\frac {r^{2}\cos(\varphi )\sin(\varphi )}{r^{2}}}=\cos(\varphi )\sin(\varphi )}$

függvényt kapjuk, ami az φ = 0 esetén a 0 értéket veszi föl, de φ = π/4-re az 1/2-et adja, így létezik két irány, amelyek felől a 0-hoz tartva az r-rel a függvényértékek sorozata nem azonos számokhoz tart.

Polárkoordinátás görbe érintője

Az ${\displaystyle r(\vartheta )}$ poláris görbe érintője meredekségének meghatározásához bármelyik pontban először írjuk át a görbe egyenletét paraméteres egyenletrendszerbe:

${\displaystyle x=r(\vartheta )\cos \vartheta \,}$

${\displaystyle y=r(\vartheta )\sin \vartheta \,}$

Mindkét egyenletet θ szerint deriválva ezt kapjuk:

${\displaystyle {\frac {dx}{d\vartheta }}=r'(\vartheta )\cos \vartheta -r(\vartheta )\sin \vartheta \,}$

${\displaystyle {\frac {dy}{d\vartheta }}=r'(\vartheta )\sin \vartheta +r(\vartheta )\cos \vartheta \,}$

A második egyenletet az elsővel osztva megkapjuk a görbe egy tetszőleges (r, ${\displaystyle r(\vartheta )}$) pontjában az érintő meredekségét a derékszögű koordináta-rendszerben:

${\displaystyle {\frac {dy}{dx}}={\frac {r'(\vartheta )\sin \vartheta +r(\vartheta )\cos \vartheta }{r'(\vartheta )\cos \vartheta -r(\vartheta )\sin \vartheta }}}$

Szektortartomány területe

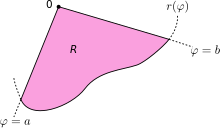
Jelölje R azt a területet, melyet az ${\displaystyle r(\vartheta )}$ görbe és a ${\displaystyle \vartheta }$ = a és ${\displaystyle \vartheta }$ = b zár közre, ahol 0 < b − a < 2π. Ekkor az R területe:

${\displaystyle {\frac {1}{2}}\int _{a}^{b}r(\vartheta )^{2}\,d\vartheta .}$

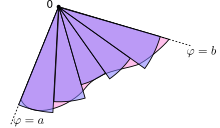
Ez az eredmény a következőképpen vezethető le. Először az [a, b] intervallumot n számú részre bontjuk, ahol n tetszőleges pozitív egész szám. Így a részek Δθ ívhossza b − a (a terület teljes ívhossza) osztva a részek számával. Minden egyes i = 1, 2, …, n résznél legyen ${\displaystyle \vartheta _{i}}$ a rész szögfelezője és szerkesszünk olyan körcikket, melynek középpontja a pólus, sugara ${\displaystyle r(\vartheta _{i})}$, középponti szöge ${\displaystyle \Delta \vartheta }$ és ívhossza ${\displaystyle r(\vartheta _{i})\Delta \vartheta \,}$. Az egyes körcikkek területe ennélfogva: ${\displaystyle {\tfrac {1}{2}}r(\vartheta _{i})^{2}\Delta \vartheta }$. Következésképpen a körcikkek összterülete:

${\displaystyle \sum _{i=1}^{n}{\tfrac {1}{2}}r(\vartheta _{i})^{2}\,\Delta \vartheta .}$

A részterületek n számának növelésével a terület közelítése javul. Ha n → ∞, az összeg a fenti integrál Riemann összegéhez tart.

Integráltranszformáció

G folytonosan differenciálható (sőt, analitikus) az értelmezési tartománya belsején, Jacobi-mátrixa:

${\displaystyle \mathrm {J} ^{G}(r,\varphi )={\begin{pmatrix}\cos(\varphi )&-r\cdot \sin(\varphi )\\&\\\sin(\varphi )&r\cdot \cos(\varphi )\end{pmatrix}}}$ és ennek determinánsa: ${\displaystyle \det \mathrm {J} ^{G}(r,\varphi )=r\,}$

Legyen tehát a kétváltozós f valós függvény integrálható egy olyan T ⊆ R×R tartományon, mely polárkoordináta-hálózathoz jól illeszkedik. Ekkor az eredetileg x és y paraméterekkel megadott T = T_x,y tartományon az integrál kiszámítását visszavezethetjük a (0,+R) × (0,2π) tégla egy feltehetőleg T-nél alkalmasabb

${\displaystyle T_{r,\varphi }=\{(r,\varphi )\in (0,+R)\times (0,2\pi )\mid (x(r,\varphi ),y(r,\varphi ))\in T_{x,y}\}}$

részhalmazán történő integráljára:

${\displaystyle \int \limits _{T_{x,y}}f(x,y)\;\mathrm {d} x\,\mathrm {d} y=\int \limits _{T_{r,\varphi }}f(x(r,\varphi ),y(r,\varphi ))\cdot r\;\mathrm {d} r\,\mathrm {d} \varphi }$

Vektoranalízis

A vektoranalízist szintén lehet alkalmazni a polárkoordinátákra. Legyen ${\displaystyle \mathbf {r} }$ egy ${\displaystyle (r\cos(\vartheta ),r\sin(\vartheta ))\,}$ helyvektor, ahol r és ${\displaystyle \vartheta }$ a t idő függvénye, ${\displaystyle {\hat {\mathbf {r} }}}$ pedig egy ${\displaystyle \mathbf {r} }$ irányú egységvektor, ${\displaystyle {\hat {\boldsymbol {\vartheta }}}}$ pedig egy ${\displaystyle \mathbf {r} }$-re merőleges egységvektor. A helyvektor idő szerinti első és második deriváltja:

${\displaystyle {\frac {d\mathbf {r} }{dt}}={\dot {r}}{\hat {\mathbf {r} }}+r{\dot {\vartheta }}{\hat {\boldsymbol {\vartheta }}},}$

${\displaystyle {\frac {d^{2}\mathbf {r} }{dt^{2}}}=({\ddot {r}}-r{\dot {\vartheta }}^{2}){\hat {\mathbf {r} }}+(r{\ddot {\vartheta }}+2{\dot {r}}{\dot {\vartheta }}){\hat {\boldsymbol {\vartheta }}}.}$

Lokális bázisvektorok és ortogonalitás

Egyenes vonalú koordináta-rendszerekben (lásd: affin koordináta-rendszer) a teljes vektortérnek van bázisa. Görbe vonalú koordináta-rendszerekben minden pontban külön bázissal kell számolni. A helyi ${\displaystyle \textstyle {\vec {b}}_{1}}$ és ${\displaystyle \textstyle {\vec {b}}_{2}}$ bázisvektorok a koordinátavonalak érintői, és a görbeegyenletekből adódnak azok paraméter szerinti deriválásával. Ugyanehhez az eredményhez eljuthatunk az ${\displaystyle {\vec {r}}}$ helyvektor koordinátatranszformációjának parciális deriválásával az ${\displaystyle r}$ és ${\displaystyle \varphi }$ koordináták szerint:

${\displaystyle {\vec {r}}={\begin{pmatrix}x\\y\end{pmatrix}}={\begin{pmatrix}r\cos \varphi \\r\sin \varphi \end{pmatrix}}}$

illetve

${\displaystyle {\vec {b}}_{1}={\frac {\partial {\vec {r}}}{\partial r}}={\begin{pmatrix}\cos \varphi \\\sin \varphi \end{pmatrix}}\quad }$ és ${\displaystyle \quad {\vec {b}}_{2}={\frac {\partial {\vec {r}}}{\partial \varphi }}={\begin{pmatrix}-r\sin \varphi \\r\cos \varphi \end{pmatrix}}}$.

A bázisvektorok hossza

${\displaystyle |{\vec {b}}_{1}|={\sqrt {{\vec {b}}_{1}{\vec {b}}_{1}}}=1\quad }$ és ${\displaystyle \quad |{\vec {b}}_{2}|={\sqrt {{\vec {b}}_{2}{\vec {b}}_{2}}}=r}$

és ortogonálisak egymásra, mivel:

${\displaystyle {\vec {b}}_{1}{\vec {b}}_{2}=0}$.

Így a koordinátavonalak merőlegesek egymásra, tehát a polárkoordináta-rendszer ortogonális koordináta-rendszer.

A tenzorszámításban a koordinátavonalakhoz érintőleges lokális koordináta-rendszerek a koordinátatranszformációk során kovariánsan viselkednek.

Metrikus tenzor

Egy kovariáns ${\displaystyle g=(g_{ij})}$ metrikus tenzor komponensei a kovariáns helyi bázisvektorok skaláris szorzatai:

${\displaystyle g_{ij}={\vec {b}}_{i}{\vec {b}}_{j}\quad (i,j\in \{1,2\})}$.

Az előző szakasz eredményeit felhasználva:

${\displaystyle g={\begin{pmatrix}1&0\\0&r^{2}\end{pmatrix}}}$.

Funkcionáldetermináns

A polárkoordinátákról az ${\displaystyle x=r\cos \varphi ,\,y=r\sin \varphi }$ Descartes-koordinátákra való áttérés funkcionáldeterminánsa a Jacobi-mátrix determinánsa:

${\displaystyle \det J=\det {\frac {\partial (x,y)}{\partial (r,\varphi )}}={\begin{vmatrix}{\frac {\partial x}{\partial r}}&{\frac {\partial x}{\partial \varphi }}\\{\frac {\partial y}{\partial r}}&{\frac {\partial y}{\partial \varphi }}\end{vmatrix}}={\begin{vmatrix}\cos \varphi &-r\sin \varphi \\\sin \varphi &r\cos \varphi \end{vmatrix}}=r\cos ^{2}\varphi +r\sin ^{2}\varphi =r}$

Felszínelem

A funkcionáldeterminánssal adódik a felszínelem polárkoordinátákban:

${\displaystyle \mathrm {d} A=\mathrm {d} x\,\mathrm {d} y=|J|\,\mathrm {d} r\,\mathrm {d} \varphi =r\,\mathrm {d} r\,\mathrm {d} \varphi }$

A felszínelem értelmezhető differenciális téglalapként, melynek szélessége ${\displaystyle r\cdot \mathrm {d} \varphi }$ és magassága ${\displaystyle \mathrm {d} r}$.

Vonalelem

A fenti

${\displaystyle x=r\cos \varphi }$

${\displaystyle y=r\sin \varphi }$

transzformációegyenletekből következik, hogy

${\displaystyle \mathrm {d} x=\cos \varphi \,\mathrm {d} r-r\,\sin \varphi \,\mathrm {d} \varphi }$

${\displaystyle \mathrm {d} y=\sin \varphi \,\mathrm {d} r+r\,\cos \varphi \,\mathrm {d} \varphi }$

A kartesiánus vonalelemre teljesül, hogy:

${\displaystyle \mathrm {d} s^{2}=\mathrm {d} x^{2}+\mathrm {d} y^{2}\,}$

amiből a polárkoordinátákra:

${\displaystyle \mathrm {d} s^{2}=\mathrm {d} r^{2}+r^{2}\,\mathrm {d} \varphi ^{2}}$

Sebesség és gyorsulás polárkoordinátákban

A mozgást sugaras és a rá merőleges érintőleges irányra bontjuk. Az ${\displaystyle {\dot {\vec {r}}}}$ sebességvektorra teljesül, hogy:

${\displaystyle {\dot {\vec {r}}}={\dot {r}}\,{\vec {e}}_{r}+r{\dot {\varphi }}\,{\vec {e}}_{\varphi }}$

ahol ${\displaystyle {\vec {e}}_{r}=(\cos(\varphi ),\sin(\varphi ))}$ és ${\displaystyle {\vec {e}}_{\varphi }=({-\sin(\varphi )},\cos(\varphi ))}$ egységvektorok.

Az ${\displaystyle {\ddot {\vec {r}}}}$ gyorsulásra:

${\displaystyle {\ddot {\vec {r}}}=({\ddot {r}}-r{\dot {\varphi }}^{2})\,{\vec {e}}_{r}+(2{\dot {r}}{\dot {\varphi }}+r{\ddot {\varphi }})\,{\vec {e}}_{\varphi }.}$

Története

A szög és a távolság fogalmakat az ókorban a Krisztus előtti első évezredben már ismerték. Hipparkhosz elsőként (190–120) állított elő húrtáblázatot (a szinusztáblázat ősét), hogy a húr hosszának ismeretében meg lehessen találni a hozzá tartozó szöget. Ennek segítségével tudott polárkoordinátákat használni, és ezzel meghatározni bizonyos csillagok helyét. Műve azonban csak a koordináta-rendszernek csak egy részét ismertette.^[1]

Arkhimédész A spirálokról című művében írt spirálokról, ahol a sugár a szög függvényében változik (lásd arkhimédészi spirál). Azonban ő sem írt a teljes koordináta-rendszerről.

Különböző leírások készültek arról, hogyan definiálható a polárkoordináta-rendszer egy formális koordináta-rendszer részeként. A téma történetét Julian Coolidge, a Harvard professzora foglalta össze Origin of Polar Coordinates című könyvében.^[2] Eszerint Grégoire de Saint-Vincent és Bonaventura Cavalieri egymástól függetlenül vezették be a fogalmat a 17. század közepén. Saint-Vincent magánjellegű feljegyzéseiben 1625-ben írt róla, és 1647-ben jelentette meg művét. Cavalieri 1635-ben adta ki az első változatot, és az újabb, javított változatot 1653-ban. Cavalieri arra használta, hogy megoldjon egy arkhimédészi spirállal kapcsolatos problémát. Később Blaise Pascal polárkoordináta-rendszerrel számította ki parabolikus szögek hosszát.

Sir Isaac Newton az 1671-ben megírt, és 1736-ban kiadott Method of Fluxions című művében polárkoordináta-rendszerek közötti transzformációkról írt, a „Seventh Manner; For Spirals“ fejezetben. Emellett még kilenc más koordináta-rendszert is bevezetett.^[3]

Jakob Bernoulli az Acta Eruditorum (1691) szakmai folyóiratban alkalmazott egy rendszert, ami egy egyenesből és egy rajta kijelölt pontból állt, melyet pólusnak nevezett. A koordinátákat a pólustól mért távolság és az egyenessel bezárt szög határozta meg. Bernoulli munkája bevezette a simulókör fogalmát is, melyet ezekkel a koordinátákkal határozott meg.

Gregorio Fontana a 18. században bevezette a polárkoordináták fogalmát az olasz nyelvbe. George Peacock 1816-ban bevezette ezt az angol nyelvbe, amikor Sylvestre Lacroix művét, a Differential and Integral Calculust fordította. ^[4][5]

Elsőként Alexis-Claude Clairaut gondolta tovább a polárkoordinátákat három dimenzióba, azonban ez végül csak Leonhard Eulernak sikerült.^[2]

Fordítás

• Ez a szócikk részben vagy egészben a Polar coordinate system című angol Wikipédia-szócikk fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.
• Ez a szócikk részben vagy egészben a Polarkoordinaten című német Wikipédia-szócikk fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.

Jegyzetek

Források

• Pattantyús Gépész- és Villamosmérnökök Kézikönyve 1. kötet. Műszaki Könyvkiadó, Budapest, 1961
• W. Werner. Vektoren und Tensoren als universelle Sprache in Physik und Technik. Springer Vieweg