Triangle de Fuhrmann

Milieux des arcs :

Le triangle de Fuhrmann, nommé d'après Wilhelm Fuhrmann (1833-1904), est un triangle spécial de la géométrie moderne du triangle.
Pour un triangle donné et son cercle circonscrit, on désigne les milieux des arcs aux côtés du triangle respectivement . Ces points médians sont reflétés sur les côtés du triangle associés, ce qui donne les points , qui forment le triangle de Fuhrmann[1],[2].
Le cercle circonscrit au triangle de Fuhrmann est le cercle de Fuhrmann. De plus, le triangle de Furhmann est similaire au triangle formé par les points milieux des arcs, c'est-à-dire [1]. L'aire du triangle de Fuhrmann s'obtient par la formule[3]:
Où désigne le centre circonscrit du triangle donné et son rayon ainsi que désignant le centre du cercle inscrit et son rayon. Grâce au théorème d'Euler, on a aussi . Les équations suivantes sont valables pour les côtés du triangle de Fuhrmann :
Où désigne les côtés du triangle donné et les côtés du triangle de Fuhrmann.
Centres du triangle de Fuhrmann
Plusieurs centres du triangle de Fuhrmann sont liés à ceux du triangle de référence : l'orthocentre du triangle de Fuhrmann est le centre du cercle inscrit de , les deux triangles ont le même centre du cercle d'Euler, etc...
Cercle de Fuhrmann
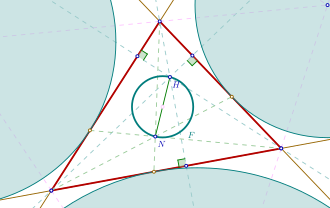

le point de Nagel et l'orthocentre
On a alors :
Le cercle de Fuhrmann d'un triangle est le cercle circonscrit au triangle de Fuhrmann de ce triangle. Un de ses diamètres est le segment entre l'orthocentre et le point de Nagel du triangle de référence[1].
Pour un triangle de côtés a, b, c et de rayon du cercle circonscrit R, le rayon du cercle de Fuhrmann vaut :
qui vaut aussi la distance entre les centres des cercles circonscrit et inscrit[4].
Le cercle de Fuhrmann coupe les hauteurs du triangle de référence en deux points, dont l'orthocentre. Les autres points sont tous à une distance des sommets du triangle de référence[2].
Le cercle de Fuhrmann est aussi appelé « cercle des huit points », car il passe par huit points remarquables du triangle, en référence à l'autre nom du cercle d'Euler, le « cercle des neuf points ». Par ailleurs, pour un triangle ABC de centre du cercle inscrit I, le cercle de Fuhrmann est le cercle circonscrit du triangle formé par les points de Nagel des triangles ABI, BCI, CAI.
Le centre du cercle de Fuhrmann a pour nombre de Kimberling X355 et admet comme coordonnées trilinéaires[5]:
Références
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Fuhrmann triangle » (voir la liste des auteurs).
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Fuhrmann circle » (voir la liste des auteurs).
- ↑ a b et c Roger A. Johnson: Advanced Euclidean Geometry. Dover 2007, (ISBN 978-0-486-46237-0), pp. 228–229, 300 (originally published 1929 with Houghton Mifflin Company (Boston) as Modern Geometry).
- ↑ a et b Ross Honsberger: Episodes in Nineteenth and Twentieth Century Euclidean Geometry. MAA, 1995, pp. 49-52
- ↑ (en) Eric W. Weisstein, « Fuhrmann triangle », sur MathWorld
- ↑ (en) Eric W. Weisstein, « Fuhrmann Circle », sur MathWorld
- ↑ (en) Eric W. Weisstein, « Fuhrmann Center », sur MathWorld
- (en) Nguyen Thanh Dung, « The Feuerbach Point and the Fuhrmann Triangle », Forum Geometricorum, vol. 16, , pp. 299–311 (lire en ligne).
- (en) J. A. Scott, « An Eight-Point Circle », The Mathematical Gazette, vol. 86, no 506, , pp. 326–328 (JSTOR 3621878)
Liens externes
- (en) Fuhrmann circle
 Portail de la géométrie
Portail de la géométrie
































