Octaèdre tronqué

Octaèdre tronqué
Description de l'image truncatedoctahedron.gif.

Éléments
Faces Arêtes Sommets
14 (8 hexagones et 6 carrés) 36 24 de degré 3
Données clés
Type Solide d'Archimède
Caractéristique 2
Propriétés Semi-régulier et convexe, zonoèdre
Dual Tétrakihexaèdre

modifier Consultez la documentation du modèle

Développement de l'octaèdre tronqué.

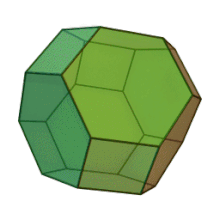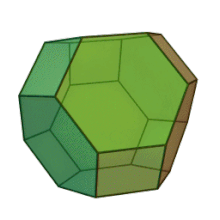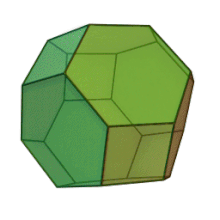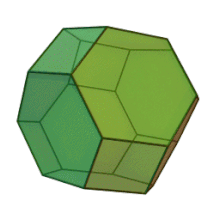
L'octaèdre tronqué, ou tétrakaidécaèdre d'Archimède[1], est un polyèdre possédant 8 faces hexagonales régulières, 6 faces carrées, 24 sommets identiques et 36 arêtes égales. Ses faces étant des polygones réguliers se rencontrant en des sommets identiques, l'octaèdre tronqué est un solide d'Archimède. Chaque face ayant un centre de symétrie, c'est aussi un zonoèdre (à six générateurs).

Comme le cube, l'octaèdre tronqué permet de paver l'espace.

Coordonnées et permutations

En effectuant les 6 × 4 = 24 {\displaystyle 6\times 4=24} permutations de (0, ±1, ±2) on obtient les coordonnées cartésiennes des sommets d'un octaèdre tronqué centré à l'origine. Les sommets sont aussi ceux de 12 rectangles dont les longueurs sont parallèles aux axes de coordonnées.

L'octaèdre tronqué peut aussi être représenté par plus de coordonnées symétriques en dimension quatre : les 24 permutations de (1,2,3,4) forment les sommets d'un octaèdre tronqué dans le sous-espace de dimension 3 x + y + z + w = 10. Pour cette raison, l'octaèdre tronqué est aussi connu quelquefois sous le nom de permutoèdre. La construction se généralise à n quelconque, et forme un polytope de dimension n – 1, ses sommets étant obtenus par les n! permutations de (1,2,..,n). Par exemple, les six permutations de (1,2,3) forment un hexagone régulier dans le plan x + y + z = 6.

Construction géométrique

Troncature de l'octaèdre régulier.
Troncature de l'octaèdre régulier.

On obtient un tétrakaidécaèdre d'Archimède (ou octaèdre tronqué) en tronquant les 6 sommets d'un octaèdre régulier à hauteur du tiers de chaque arête.

On peut aussi construire un octaèdre tronqué à l'aide du patron ci-contre.

Mesures et volume

Si les arêtes de l'octaèdre tronqué sont de longueur a,

  • son volume est :
V = 8 2   a 3 ≈ 11,313 7   a 3 {\displaystyle V=8{\sqrt {2}}\ a^{3}\approx 11{,}3137\ a^{3}}
Démonstration

L'octaèdre dont provient l'octaèdre tronqué a pour longueur d'arête b = 3 a {\displaystyle b=3a} . On peut le voir comme la réunion de deux pyramides de base carrée (d'arête b) et de hauteur b 2 2 {\displaystyle \textstyle b{\frac {\sqrt {2}}{2}}} , donc de volume v 0 = 1 3 ( b 2 2 ) b 2 = b 3 2 6 {\displaystyle \textstyle v_{0}={\frac {1}{3}}\left(b{\frac {\sqrt {2}}{2}}\right)b^{2}=b^{3}{\frac {\sqrt {2}}{6}}} . Chacune des 6 petites pyramides retirées de l'octaèdre était 3 fois plus petite donc 33 = 27 fois moins volumineuse : v 1 = v 0 / 27. {\displaystyle v_{1}=v_{0}/27.} Le volume de l'octaèdre tronqué est donc : V = 2 v 0 − 6 v 1 = ( 2 − 6 27 ) b 3 2 6 = 8 27 2   b 3 = 8 2   a 3 . {\displaystyle \textstyle V=2v_{0}-6v_{1}=\left(2-{\frac {6}{27}}\right)b^{3}{\frac {\sqrt {2}}{6}}={\frac {8}{27}}{\sqrt {2}}\ b^{3}=8{\sqrt {2}}\ a^{3}.}

  • l'aire de sa surface est :
A = 6 ( 1 + 2 3 )   a 2 ≈ 26,784 6   a 2 {\displaystyle A=6\,(1+2{\sqrt {3}})\ a^{2}\approx 26{,}7846\ a^{2}}
Démonstration

La surface de l'octaèdre tronqué est composée de 6 faces carrées et 8 faces hexagonales, chacune de côté a. Chaque carré est d'aire A c = a 2 . {\displaystyle A_{\mathrm {c} }=a^{2}.} On peut voir chaque hexagone comme la réunion de 6 triangles équilatéraux de côté a donc d'aire A t = 1 2 ( a ) ( a 3 2 ) = a 2 3 4 {\displaystyle \textstyle A_{\mathrm {t} }={\frac {1}{2}}(a)\left(a{\frac {\sqrt {3}}{2}}\right)=a^{2}{\frac {\sqrt {3}}{4}}}  : l'aire de chaque hexagone est A h = 6 A t = 3 3 2 a 2 . {\displaystyle \textstyle A_{\mathrm {h} }=6A_{\mathrm {t} }={\frac {3{\sqrt {3}}}{2}}a^{2}.} L'aire totale est donc finalement : A = 6 A c + 8 A h = ( 6 + 12 3 )   a 2 . {\displaystyle \textstyle A=6A_{\mathrm {c} }+8A_{\mathrm {h} }=(6+12{\sqrt {3}})\ a^{2}.}

Notes et références

  1. ↑ Un tétrakaidécaèdre est un polyèdre possédant 14 faces.

Voir aussi

Bibliographie

  • (en) Robert Williams, The Geometrical Foundation of Natural Structure: A Source Book of Design, 1979, (ISBN 0-486-23729-X)
  • (en) Mathworld : the truncated octahedron

Liens externes

  • (en) [1]
  • (en) Polyèdres virtuels : l'encyclopédie des polyèdres
  • (en) [2]
  • (en) [3]
v · m
Solides de Platon (5)
Solides d'Archimède (13)
Solides de Kepler-Poinsot (4)
Solides de Catalan (13)
Solides de révolution
Composés polyédriques
Solides de Johnson (92) voir Modèle:Palette Solides de Johnson
  • icône décorative Portail de la géométrie