Teorema de Apolonio

En geometría, el teorema de Apolonio, también llamado teorema de la mediana, es un teorema que relaciona la longitud de la mediana de un triángulo con las longitudes de sus lados.

Para cualquier triángulo ΔABC (véase fig. 1), si M es la mediana correspondiente al lado c, donde AP = PB = ½ c, entonces:

${\displaystyle a^{2}+b^{2}={\frac {1}{2}}\;c^{2}+2\;M^{2}}$

Afinidades

• Este teorema es un caso especial del teorema de Stewart.
• Para triángulos isósceles el teorema se reduce al teorema de Pitágoras.
• Teniendo en cuenta que las diagonales del paralelogramo se bisecan entre sí, puede concluirse que este teorema es equivalente a la ley del paralelogramo.
• El nombre de este teorema es en alusión a Apolonio de Perga.^[1]​

Sobre las demostraciones

Existen (o pueden existir) razones para no exponer las demostraciones originales, una de ellas sería que los documentos de dichas demostraciones no hayan llegado hasta nuestros días. Por otra parte, al existir en nuestros días más y mejores herramientas matemáticas, puede optarse (aplicando el principio de parsimonia) por exponer solo las demostraciones más sencillas.

Al igual que muchos otros teoremas este puede ser demostrado de múltiples maneras, algunas de ellas serían:

• Como caso especial del teorema de Stewart.
• Usando vectores (véase ley del paralelogramo).
• Usando el teorema del coseno.

Demostración de Godfrey y Siddons

Demostración^[2]​ por medio del teorema del coseno. Sea un triángulo euclidiano cualquiera de lados a, b y c, para cuyo lado c se ha trazado la mediana correspondiente M_c (línea verde en la fig. G&S), donde (por definición de mediana) m_c = n_c = ½ c. La mediana M_c forma con el lado c los ángulos φ y φ', siendo que φ abarca al lado b y φ' abarca al lado a, entonces de acuerdo al teorema del coseno podemos expresar:

(gs01)${\displaystyle b^{2}=m_{c}^{2}+M_{c}^{2}-2\;m_{c}\;M_{c}\;\cos(\varphi )}$

(gs02)${\displaystyle a^{2}=n_{c}^{2}+M_{c}^{2}-2\;n_{c}\;M_{c}\;\cos(\varphi ')}$

Reemplazando en (gs01) m_c → ½ c y en (gs02) n_c → ½ c y cos φ'  →  -cos φ (por ser φ' y φ ángulos suplementarios), y simplificando obtenemos:

(gs03)${\displaystyle b^{2}={\frac {c^{2}}{4}}+M_{c}^{2}-2\;{\frac {c}{2}}\;M_{c}\;\cos(\varphi )}$

(gs04)${\displaystyle a^{2}={\frac {c^{2}}{4}}+M_{c}^{2}+2\;{\frac {c}{2}}\;M_{c}\;\cos(\varphi )}$

Notar que los últimos términos de los miembros derechos de las ecuaciones (gs03) y (gs04) solo difieren en signo, luego sumando m.a. m. dichas ecuaciones y simplificando arroja:

(gs05)${\displaystyle a^{2}+b^{2}={\frac {c^{2}}{2}}+2M_{c}^{2}}$

  , ∎.^[3]​

La expresión anterior (gs05) es la conclusión final del teorema de Apolonio realizada para la mediana M_c, como se trata de una demostración general, con razonamientos similares se puede obtener las expresiones equivalentes para las restantes medianas M_a y M_b, las cuales serían:

(gs06)${\displaystyle b^{2}+c^{2}={\frac {a^{2}}{2}}+2M_{a}^{2}}$

(gs07)${\displaystyle a^{2}+c^{2}={\frac {b^{2}}{2}}+2M_{b}^{2}}$

Fórmulas de aplicación práctica

De las expresiones (gs05), (gs06) y (gs07) de la demostración (Godfrey y Siddons) del teorema de Apolonio (teorema de las medianas) pueden deducirse varias fórmulas prácticas (válidas para cualquier triángulo), éstas permiten calcular a partir del conocimiento de tres elementos , a un cuarto elemento desconocido, (los elementos en cuestión son lados y medianas) . La siguiente tabla muestra un resumen de las mismas (con notación acorde a la figura de la propia tabla ):

Triángulos — Medianas ( fórmulas prácticas II )

${\displaystyle M_{a}={\frac {1}{2}}{\sqrt {2\left(b^{2}+c^{2}\right)-a^{2}}}}$
${\displaystyle M_{b}={\frac {1}{2}}{\sqrt {2\left(a^{2}+c^{2}\right)-b^{2}}}}$
${\displaystyle M_{c}={\frac {1}{2}}{\sqrt {2\left(a^{2}+b^{2}\right)-c^{2}}}}$
${\displaystyle a={\sqrt {2\left(b^{2}+c^{2}\right)-4M_{a}^{2}}}}$	${\displaystyle b={\sqrt {{\frac {a^{2}}{2}}-c^{2}+2M_{a}^{2}}}}$	${\displaystyle c={\sqrt {{\frac {a^{2}}{2}}-b^{2}+2M_{a}^{2}}}}$
${\displaystyle a={\sqrt {{\frac {b^{2}}{2}}-c^{2}+2M_{b}^{2}}}}$	${\displaystyle b={\sqrt {2\left(a^{2}+c^{2}\right)-4M_{b}^{2}}}}$	${\displaystyle c={\sqrt {-a^{2}+{\frac {b^{2}}{2}}+2M_{b}^{2}}}}$
${\displaystyle a={\sqrt {-b^{2}+{\frac {c^{2}}{2}}+2M_{c}^{2}}}}$	${\displaystyle b={\sqrt {-a^{2}+{\frac {c^{2}}{2}}+2M_{c}^{2}}}}$	${\displaystyle c={\sqrt {2\left(a^{2}+b^{2}\right)-4M_{c}^{2}}}}$
( Lados: a, b y c ) — ( Medianas: Ma, Mb y Mc )[4]​ — ( Semilados: ma=na = ½ a , mb=nb = ½ b y mc=nc = ½ c ).

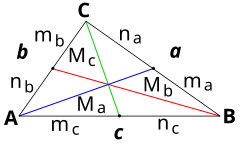Véase también

• Teorema de Stewart
• Teorema de Ceva
• Ley del paralelogramo
• Mediana (geometría)
• Triángulo

Notas y referencias

• Apollonius Theorem en PlanetMath.