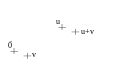En álgebra lineal, un subespacio vectorial es el subconjunto de un espacio vectorial, que satisface por sí mismo la definición de espacio vectorial con las mismas operaciones que V el espacio vectorial original.
Definición de subespacio vectorial
Sea  un espacio vectorial sobre
un espacio vectorial sobre  y
y  no vacío,
no vacío,  es un subespacio vectorial de
es un subespacio vectorial de  si:
si:


Consecuencias
- Un subconjunto de vectores que cumple las dos condiciones anteriores es un subespacio vectorial y por tanto un espacio vectorial.
Notaciones
Dado  un subespacio vectorial, se tiene:
un subespacio vectorial, se tiene:
Para i) el abuso de lenguaje  , e incluso
, e incluso  es correcto.
es correcto.
| Demostración |
Se quiere ver que  : : 

|
Para ii) el abuso de lenguaje  , e incluso
, e incluso  es correcto.
es correcto.
| Demostración |
 |
Criterio de verificación
Es posible sintetizar i) y ii) en una condición única:
Si V es un espacio vectorial, entonces un subconjunto no vacío U de V es un subespacio vectorial si y sólo si para cualesquiera dos vectores v, w pertenecientes a U y cualesquiera escalares r y s pertenecientes al cuerpo asociado, el vector  es también un elemento de U. es también un elemento de U. |
Ejemplos
Dado el espacio vectorial  , sus elementos son del tipo
, sus elementos son del tipo  .
.
-

y

están alineados,

,

-

y

forman un paralelogramo si no están alineados,

-
Suma de 3 elementos.
El subconjunto
 .
.
es un subespacio vectorial.
| Demostración |
Por definición de U los elementos son de la forma  . .


como las operaciones están bien definidas entonces U es en sí mismo un espacio vectorial, es decir, satisface las condiciones de subespacio vectorial de  . .
|
El subconjunto

no es un subespacio vectorial.
| Demostración |
| Nuevamente sólo es necesario verificar tres condiciones: la pertenencia del vector nulo y la cerradura de ambas operaciones. El vector nulo (0, 0) sí es un elemento de C puesto que 0 = 0². Sin embargo, ni la suma ni el producto son cerrados: - Los vectores (1, 1) y (2, 4) son elementos de C, pero su suma (1, 1) + (2, 4) = (3,5) no lo es, puesto que 5 no es igual a 3².
- El vector (2, 4) es un elemento de C, pero al multiplicarlo por el escalar 2 se obtiene (4, 8) que no es un elemento de C puesto que 8 no es igual a 4².
|
Otros ejemplos
Sea  un espacio vectorial. Asumimos que
un espacio vectorial. Asumimos que  es un espacio vectorial real, pero todo funciona también para un espacio vectorial complejo.
es un espacio vectorial real, pero todo funciona también para un espacio vectorial complejo.
1) {0} es un subespacio vectorial de  . Es llamado el subespacio trivial de
. Es llamado el subespacio trivial de  .
.
2)  en sí es un subespacio vectorial de
en sí es un subespacio vectorial de  .
.
3) Si fijamos 
 . Entonces el conjunto
. Entonces el conjunto  es un subespacio de
es un subespacio de  .
.
4) Más generalmente, si fijamos  , ...,
, ..., 
 , entonces el conjunto
, entonces el conjunto  es un subespacio de
es un subespacio de  . Este conjunto es llamado el generador lineal de
. Este conjunto es llamado el generador lineal de  , ...,
, ...,  .
.
5) Si fijamos  y
y  , ...,
, ..., 
 , entonces el conjunto
, entonces el conjunto 



 es un subespacio afín de
es un subespacio afín de  . En general, no será un subespacio.
. En general, no será un subespacio.
6) Si  es un subespacio de
es un subespacio de  , entonces
, entonces  no es un subespacio. Esto es fácil de ver, considerando que
no es un subespacio. Esto es fácil de ver, considerando que  debe que contener el 0, pero
debe que contener el 0, pero  no contiene el 0. Por lo tanto, no puede ser un espacio vectorial.
no contiene el 0. Por lo tanto, no puede ser un espacio vectorial.
Operaciones con subespacios
Sea  un espacio vectorial;
un espacio vectorial;  y
y  subespacios vectoriales de
subespacios vectoriales de  , se definen las siguientes operaciones:
, se definen las siguientes operaciones:
Unión

En general, la unión de subespacios no es un subespacio.
Intersección

La intersección de dos subespacios es un subespacio.
Suma

La suma de dos subespacios es un subespacio de V.
Suma directa
Si la intersección entre S y W es el subespacio trivial (es decir, el vector nulo), entonces a la suma se la llama "suma directa".[1]
Es decir que si 
Esto significa que todo vector de S+W, se escribe de manera única como la suma de un vector de S y otro de W.
Subespacios suplementarios
Se dice que los subespacios  y
y  son suplementarios cuando verifican que su suma directa es igual al espacio vectorial
son suplementarios cuando verifican que su suma directa es igual al espacio vectorial  :
:

Dimensiones de subespacios
La fórmula de Grassmann resuelve que la dimensión de la suma de los subespacios  y
y  será igual a la dimensión del subespacio
será igual a la dimensión del subespacio  más la dimensión del subespacio
más la dimensión del subespacio  menos la dimensión de la intersección de ambos, es decir:
menos la dimensión de la intersección de ambos, es decir:

Por ejemplo, siendo  y
y  y teniendo como intersección un subespacio de dimensión 1.
y teniendo como intersección un subespacio de dimensión 1.
Luego,  .
.
En la suma directa
En el caso particular de la suma directa, como  .
.
La fórmula de Grassmann resulta:

Entonces en el ejemplo anterior, resultaría  .
.
Véase también
Referencias
- ↑ "Álgebra II" Armando O. Rojo. Editorial "El Ateneo". Buenos Aires.
| Control de autoridades | - Proyectos Wikimedia
 Datos: Q728435 Datos: Q728435
|
|---|
 Datos: Q728435
Datos: Q728435
 y están alineados, ,
y están alineados, ,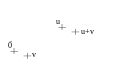 y forman un paralelogramo si no están alineados,
y forman un paralelogramo si no están alineados, Suma de 3 elementos.
Suma de 3 elementos. Portal:Matemática. Contenido relacionado con Matemática.
Portal:Matemática. Contenido relacionado con Matemática. Datos: Q728435
Datos: Q728435